1. 引言
      PID（比例-积分-微分）控制器作为最早实用化的控制器已有50多年历史，因其具有算法简单、鲁棒性好、可靠性高、直观性好等优点被广泛的应用于工业过程控制及运动控制中[1]。常规PID控制效果的优劣，不仅仅取决于控制系统模型的精确程度，还必须调整好三个参数的关系，而这种关系不一定是简单的线性组合。实际的工业过程及运动过程往往具有时变性、变参数、变结构等不确定性及很强的非线性，精确的数学模型难以建立，此外，常规PID还有实现在线调整困难，参数间相互影响，参数整定时间长等缺点，难以取得理想的控制效果。
      随着控制理论的发展，将应用广泛的PID控制器与智能控制理论相结合[2]成为智能控制研究的新方向，神经网络算法具有逼近任意非线性表达能力，很强的自学习能力和概括推广能力，在解决高度非线性和不确定系统方面有很大的的潜能，应用神经网络，可以从复杂的PID三个参数组合中寻求最佳的线性组合，使神经网络和PID本质结合。从而使得控制器具有较好的自适应性，实现参数的自动实时调节，适应过程的变化，提高系统了的鲁棒性和可靠性。
2. BP神经网络
2.1 BP神经网络的构成及设计[3]
      BP神经网络是一种具有三层或三层以上的神经网络，包括输入层、隐含层、输出层，上下层之间实现全连接，而每层神经元之间无连接。当一对学习样本提供给网络后，神经元的激活值从输入层经各中间层向输出层传播，在输出层的各神经元获得网络的输入响应。接下来，按照减少目标输出与实际误差的方向，从输出层经过各中间层逐层修正各连接权值，最后回到输入层，这种算法即BP算法。随着这种误差逆的传播修正不断进行，网络对输入模式响应的正确率也不断上升。
（1）输入输出层的设计
      输入层的设计可以根据需要求解的问题和数据表示方式确定，若输入信号为模拟波形，那么输入层可以根据波形的采样点数目撅腚输入单元的维数，也可以用一个单元输入，这是输入样本为采样的时间序列。输出层的维数可以根据使用者的要求确定。如果BP网络用作分类器，类别模式一共有m个，那么输出层神经元的个数为m或者。
（2）隐层的设计
      隐层单元的数目与问题的要求、输入/输出单元的数目都有直接的关系，隐单元的数目太多会导致学习时间过长、误差不一定最佳，也会导致容错性差、不能识别以前没有的样本等等，因此，一定存在一个最佳的隐单元数，通常用以下三个公式来选择最佳隐单元数：
1），其中k为样本数，n为输入单元数。
2），其中m为输出神经元数，n为输入单元数，a为[1,10]之间的常数。
3），其中n为输入单元数。
2.2 典型神经网络结构
一个典型的三层神经网络结构如下图所示：

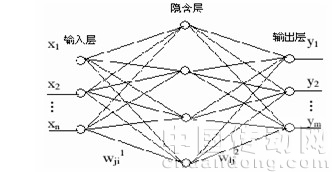
图1  BP神经网络结构图

      其中： 、 、…、 为 BP网络的输入； 、 、…、 为 BP网络的输出，对应PID控制器的三个参数；为输层到隐含层的连接权值；为隐含层到输出层的连接权值。通过神经网络的自学习、加权系数的调整，使神经网络输出对应于某种最优控制规律下的PID控制器参数。 
图一中各参数之间的关系[4]如下：
输入层：

隐含层：    
输出层：    
取性能指标为：，按照梯度下降法修正网络的权值，使最小，修正方法如下：
隐含层：     
输出层：     

[1] [2]  下一页