·上一文章：一种双CAN口同步通讯板的设计
·下一文章：单层膜ITO实现多点触摸的设计方案
由i 矢量可求出：
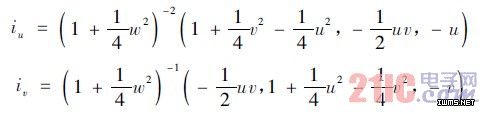
将以上三式带入反射定律，并定义p = ρu，q =ρv，可求得T = T （ u，v，ρ，p，q） ，则反射光线反射到照明面上的点的坐标为：
其中：
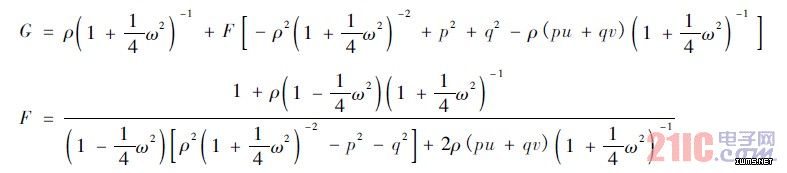
2. 2 能量守恒
LED 照明面垂直于z 轴朝下，本文采用朗伯体LED 光源，发出的光一部分直接照到照明面上，另一部分被反射后照射到照明面上，在照明面上产生一个长和宽分别为a 和b 的矩形均匀照明区域。根据能量守恒，光源的辐射通量应等于照明面上的辐射通量。
光源辐射到照明面上的辐射通量为Φ1 =∫I0 cosΦdΩ1 + ∫μI0 cosΦdΩ2，式中第一项为直接照射到照明面上的辐射通量，Ω1为该部分入射光线对应的立体角，第二项为经过反射面反射到照明面上的辐射通量，Ω2为该部分入射光线对应的立体角，μ 为反射面的反射系数。照明面上接收到的辐射通量为Φ2 = ∫ EdS，E 为照明面上的平均照度，根据能量守恒有Φ1 = Φ2。由于反射面的反射率可以高达95%以上，这里为了简单起见，不考虑反射能量损失，且郎伯型光源的发光角度为120 度， 则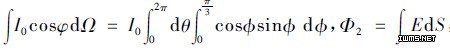
，有Φ1 = Φ2，所以E = πI0 /4ab。
照到t 点的光有两束， 一束为图示的T 光线，另一束为图示的I 光线的反射光线，则有E = E1 +E2，其中E1为T 光束在t 点产生的照度，E2为B光束产生的照度。
如图3 所示，设点光源的发光强度为I，被照射面积元dS′对它所张的立体角为dΩ，则照射在dS′上的光通量为dΦ′ = IdΩ = IdS′cosθ′，从而照度为E=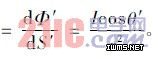
由此可求出直接照射在照明面上的光束T 在t点的照度为：
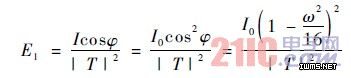
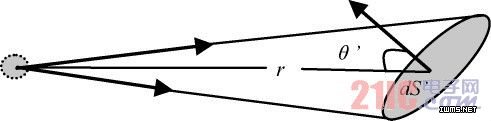
图3 光源的照度
