2.1.2基于内阻的SOC估计方法
    随着放电过程的进行，蓄电池中活性物质减少，导致蓄电池内阻增加。因此，蓄电池内阻可作为判定蓄电池容量大小的有效指标。图6是蓄电池的简化等效电路图，R1是内阻，R2是极化内阻，C等效于电容的作用，他们都与SOC有密切关系。电池在不同的SOC或SOH状态下，其内阻值是不一样的，内阻法就是通过测量蓄电池在放电过程中内阻的变化来预测SOC的变化。

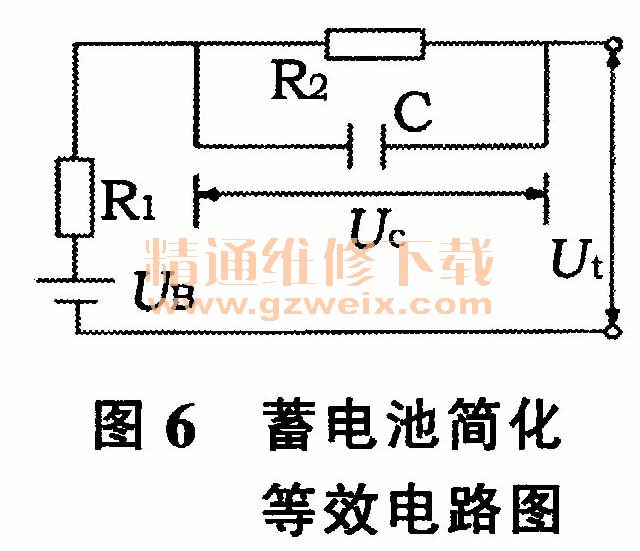
    用蓄电池的简化等效电路图分析其工作过程。蓄电池的端电压可表示为

    稳定状态下，又可表示为
   U1=Ub-I·（R1+R2）     （4）
    因此，内阻可以通过式（5）获得

    图7是对某一型号的铅酸蓄电池进行恒流20 A放电试验，得到的内阻变化曲线。

    在IEEE 1188-1996标准中，也提出了测量内阻的必要性，明确规定了电池内阻测试至少每季度进行一次。通过试验测试和理论计算对蓄电池内阻与剩余容量的关系进行了研究分析，结果表明：①铅酸蓄电池SOC在45％以上时，其内阻与充放电时间呈线性关系，当SOC低于45％时，蓄电池的内阻才很快升高；②对于容量在80％以上的实际运行车辆使用的蓄电池，内阻基本不变，此时可不根据内阻值检测蓄电池的SOC ;③根据蓄电池内阻值，可以在一定程度上确定蓄电池性能。
    按车辆实际使用和售后服务情况来看，主要将内阻法应用于判断铅酸蓄电池是否失效，实际使用过程中服务人员一般依据铅酸蓄电池的内阻来判断蓄电池是否损坏、短路、极板脱落等内部故障，直接应用于SOC预测的很少。试验发现：①单体电池的内阻值为理论计算值的80％以上时，蓄电池正常，此时蓄电池SOC≥ 80%;②当内阻值为理论计算值的60%～80％时，SOC基本不足80%，蓄电池处于“普通危险”状态，需要维护；③当内阻值为理论计算值的60％以下时，蓄电池处于“严重危险”状态，需要及时更换。

    2.1.3基于安一时法SOC估计方法
    安一时法是SOC估算最常用的方法，计算公式如式（6）

    式中：C----额定容量，以C20容量计算；刀—充放电效率且不是常数（充电时电流方向为正，此时刀为正；放电时电流方向为负，此时刀为负）。
    图8为试验中恒流20 A放电情况下铅酸蓄电池的放电电流、电压、soc状态之间的关系图，其中深色区域部分就是的积分变化情况。

    安-时法实质是将电池看作一个“黑箱”，认为流进电池的电量与流出电池的电量有一定的比例关系，而不考虑电池内部的结构和外部的电气特性，因此这种方法适用于各种电池。安一时法在应用中存在的问题：①要求标定SOC初始值；②需要精确计算充放电效率；③需准确测量电流，电流测量不准，将造成Soc计算误差，长期存在电流积分的累计误差。
    在实际应用场合采用安一时法时，一般根据使用环境和条件考虑对充放电率、温度、电池老化以及自放电率等因素进行补偿，与其他Soc估算方法配合使用。

    2.1.4基于经验方程的传统辨识模型SOC估算方法
    基于开路电压法、内阻法和安一时法的优缺点，提出一种经验方程的蓄电池SOC辨识模型，以端电压和内阻为输人参量对SOC进行辨识。其模型方程为式（7）

    由于受各种因素的干扰，内阻实测值波动较大。因此，可尝试对式（7）进行改进，以降低噪声对辨识结果造成的误差。根据工程应用中信号处

    仿真分析及验证：首先对蓄电池进行恒流放电试验，通过采集蓄电池端电压、内阻及相对应的蓄电池SOC检测得到实测数据。将实测得到的数据分别载人Lab View仿真分析，得到端电压和内阻的补

    表2中的系数带人方程（7）和方程（8），通过对电压仿真信号和内阻仿真信号的运算，估测得到方案一和方案二下的蓄电池SOC值，将之与蓄电池SOC实测信号曲线进行对比，如图9所示。



    由图9可见，方案二优于方案一，从而验证了对端电压和内阻补偿因子的改进可以有效抑制噪声对预测结果造成的误差。直观地表明了基于经验方程的传统辨识模型SOC估算方法提高了辨识精度，具有较强的实用价值，值得推广和应用。
    在实际应用和设计过程中，以基于经验方程的传统辨识模型SOC估算方法为设计基础，结合开路电压法、内阻法和安一时法设计IBS，可有效避免单一算法带来的误差。同时，实际设计和应用过程中，在不同环境下可有偏重，使得设计应用变得方便可行。

上一页  [1] [2] [3] [4]  下一页