二、试验验证
    为了研究此副箱主轴心部硬度与承载能力之间的关系，通过静扭试验台对此副箱 主 轴 进 行静 扭 强 度 试验。

    本文选取 10 根副箱主轴进行试验，对其编号分别为 1#、2#……、10#，试验过程中要求其承载工作面与汽车前进工况相同，即副箱主轴 2端只承受扭矩，不允许有任何附加弯矩作用。图 1 是 1# 轴试验过程中扭角与扭矩对应曲线，图 2 是静扭试验中被破坏的轴。

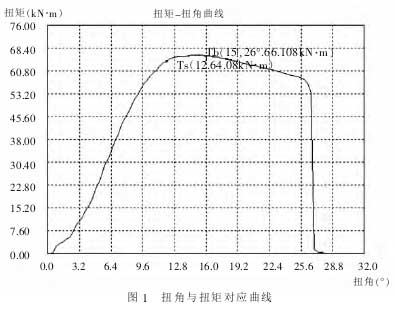
    从图 1、图 2 可以看出，试件断口截面与轴线垂直，断口平整，有回旋状变形痕迹，是切应力造成的切断，且断口无粘连现象。说明副箱主轴在试验过程中首先出现塑性变形，超过材料的屈服极限，产生破坏。

    三、试验结果与分析
    表 2 是 1# 到 10# 测试轴对应的屈服扭矩 Ts、最大扭矩 Tb 及分析后对应编号的心部硬度。
    从表 2 试验数据中，可看出屈服扭矩 Ts、最大扭矩 Tb 值较大的试件，其心部硬度高，如试件 1#、4#，其屈 服 扭 矩 Ts 所 属 范 围 在 64000 ~65600N·m 之间，心部硬度为 40.5；试件 3# 和 6# 屈服扭矩 Ts 在 55000~57600N·m 之间，心部硬度为 34.5。

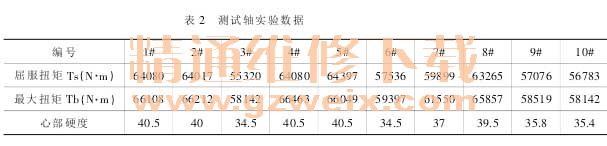
    图 3 是试件 1# 到 10# 其心部硬度与屈服扭矩 Ts、最大扭矩 Tb 对应关系。

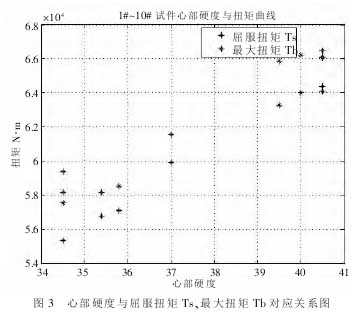
    从图 3 可以看出，心部硬度与屈服扭矩有线性对应关系，按照最小二乘法拟合后，得到心部硬度 X 与屈服扭矩 Ts 的关系为：
    Ts =1382.2*X +8370
    表 3 是根据上述公式计算得到的屈服扭矩和与测试数据差值，图 4 是测试数据与拟合值对比曲线。

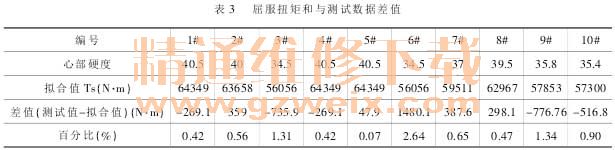
    从表 3 可知，6#试件拟合的屈服扭矩与实测数据相差最大，为 1480.1 N·m，误差为 2.64%，5#试 件 误 差 最 小 ，为0.07%，说明在副箱主轴材料、尺寸确定的情况下，根据副箱主轴屈服扭矩可大致估计其心部硬度，同时也可根据心部硬度大致估计其屈服扭矩。

    四、总结
    通过上述试验与分析，说明 12 挡变 速 器 ， 材 料 为17Cr Ni Mo6 的 副 箱主轴其心部硬度和扭矩存在线性关系，不需要进行静扭试验，可通过分析其心部硬度，估计该副箱主轴的屈服扭矩，为设计者提供参考，具有一定的实用价值。

上一页  [1] [2]