摘要：本文根据单稳态永磁真空断路器结构特点，采用虚拟样机技术，进行基于Maxwell、MATLAB、ADAMS的断路器合分闸动态仿真。先使用Maxwell建立有限元模型，计算电磁力和电感等；然后将计算结果导入MATLAB、藕合电压平衡方程与抓械运动方程，求解得到永磁真空断路器合闸动态特性仿真结果；随后采用ADAMS对永磁真空断路器分闸过程进行仿真计算；最后对实际样机进行测试，验证了仿真的正确性。

    真空断路器是中压配电网中不可或缺的开关设备。目前，一种电磁驱动、永磁保持、电子操控的永磁机构真空断路器已广泛应用于中压配电网。永磁机构相比传统操作机构，结构简单、可靠性高，使真空断路器产品向长寿命、免维护等更高要求发展成为可能。然而，永磁机构动态特性较为复杂，永磁真空断路器分合闸过程中不仅有机械运动部分的动态特性参数，还存在线圈电流、电磁力等参数的相互藕合。因此，研究永磁机构真空断路器动态特性，对于优化产品设计，提高产品性能，保证产品在电网中稳定运行就具有重要的意义。本文以某12kV户外永磁真空断路器为研究对象，进行合分闸过程的动态仿真分析，并进行实际样机试验，以保证仿真结果的准确性。

    1 永磁真空断路器模型建立与运动分析
    1.1永磁真空断路器建模
    12kV户外永磁真空断路器结构如图1所示。该断路器为柱式结构，配有单稳态永磁操作机构（合闸保持由永磁吸合力提供，分闸保持由分闸弹簧力提供），分闸弹簧置于单稳态永磁操作机构内部；传动部分采用驱动轴旋转、三相联动方式。该断路器所要求的机械特性见表1。在三维实体造型软件Solidworks中建立永磁真空断路器实体模型。



    1.2永磁真空断路器的运动分析
    永磁真空断路器的永磁机构中装有合分闸线圈，由充电电容放电励磁。单稳态永磁机构结构如图2所示。合闸时，线圈通电，永磁机构的动铁芯在电磁力、永磁体吸力共同作用下驱动主轴旋转，完成永磁真空断路器合闸操作，同时为分闸弹簧储能。合闸到位后，永磁体产生永磁保持力将永磁真空断路器保持在合闸状态。分闸时，线圈通过反向电流，产生的磁场与永磁体磁场反向抵消，动铁芯受分闸弹簧力和触头压力驱动，完成永磁真空断路器分闸操作。

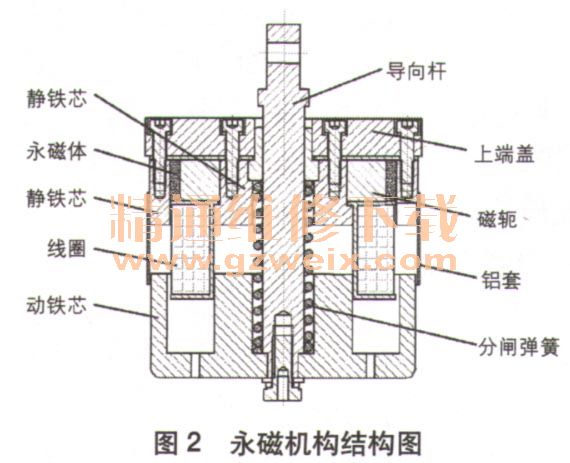
    永磁机构的动态过程在电路上遵循电压平衡方程，在运动上遵循达朗贝尔运动方程，在磁场上遵循麦克斯韦方程。这些方程间相互关联，可构成描述动态特性的微分方程组。
    式中，Uc为充电电容电压；i为线圈电流；R为线圈电阻；φ为电磁系统总磁链；L为线圈自感，是线圈电流i和铁芯位移二的函数，即L= f （x、i）；m为运动部分质量归算到铁芯上的等效质量；Fx为铁芯受到的电磁力；Ff为铁芯受到的运动反力；v为铁芯的运动速度；t为动作时间。各变量的初始条件为：φ|t=0，L|t=0，Uc|t=0=UC0，v|t=0=0，x|t=0=0，t|t=0=0。求解永磁机构的动态特性即求解式（1）。

    1.3运动反力和传动比的归算
    铁芯受到的运动反力Ff，在开距阶段为触头自闭力、运动部分（含动触头）的重力、分闸弹簧力，在超程阶段为触头自闭力、运动部分（不含动触头）的重力、分闸弹簧力、触头弹簧力，因此运动反力Ff和运动部分质量m的关系在计算时分为2个阶段来表达。驱动轴上设计有永磁机构输入拐臂与三相驱动输出拐臂，两者力臂长度比为1.69：1，即铁芯运动速度除以1.69就等于三相触头的运动速度。

[1] [2]  下一页