·上一文章：通用EV-1型电动轿车技术详解
·下一文章：变电站二次回路仿真实训系统建设与应用
根据分布参数对波形特征的影响可知，在一定频率以上需考虑分布参数的影响，且分布参数的存在可改变波形的形状。由测量高频脉冲电流的Rogowski线圈分布参数对高频频率特性影响较大可知，频率较高时需考虑线圈分布参数对波形的影响。
从已有的相关文献可知，分布参数可能是造成脉冲电流波前VFTC的主要原因。鉴于试验过程中，导线与导线之间、导线与地之间有分布电容的存在，以及导线自身存在分布电感，脉冲电流波前的VFTC产生原因从分布参数出发进行研究。而实际电路中，分布电容和分布电感通常无法通过测量设备直接测取，只有一些特殊的线路模型才可通过计算求得，如平行导线对、单根导线对地、同轴电缆等之间的分布参数可通过相应的分布参数计算式求得。由于实际试验电路的连接相对繁琐，使得分布参数的计算变得更加困难，因此不能对分布参数进行定量分析，只能进行定性分析。
2 电路仿真
由于实际电路中只有测量回路使用同轴传输线将脉冲电流传送至示波器中，因此在电路仿真中主要针对测量回路的同轴传输线波阻抗的不匹配现象进行仿真探究。在仿真电路中不存在脉冲电流测量安全因素的考虑，故将脉冲电流的测量直接采用电流探针串接于放电回路中。为了使得仿真试验结果更具有可比性，需将仿真电路的模型与实际电路尽量保持一致。
下面基于电容储能式脉冲电流放电试验装置建立对应的仿真电路模型。由于本文的目的在于探究脉冲电流波前VFTC的产生原因，因此仿真电路模型的建立只需从放电回路模型着手，即在放电开关闭合时，电容在预充电压作用下向调波电感和调波电阻放电的试验过程。由于试验过程中常采用两种电路模型，因此仿真电路中采用这两种电路模型，即由脉冲电容、调波电阻、调波电感、同轴传输线、开关所组成的串联电路和由脉冲电容、调波电阻、同轴传输线、开关所组成的串联电路。鉴于电路中导线、电感、脉冲电容等器件均为电感、电阻和电容的组合体，故本文仅对前者进行仿真讨论，而对后者不做探究。
根据实际电路中同轴传输线的长度，可计算出电磁波在同轴传输线中的传输时间，从而为电路模型的建立提供参数。试验所用的同轴电缆的长度为1. 8m，电流波在同轴传输线的传播速度为3×10 8m/s，则传输时间为6ns;开关的转换时间设置为100ns，开关器件的断开阻抗与闭合阻抗分别为1000MΩ, 0.2Ω。实际测量电路中采用100：1的Rogowski线圈采集电流数据，即所测得的脉冲电流幅值为实际脉冲电流幅值的百分之一，而波形保持不变，因此本文将脉冲电容两端的电压设置为实际电压的百分之一，即脉冲电容器的初始电压值设定为70kV×0. 01=0. 7kV。
当同轴传输线末端不加匹配阻抗时，依据电路参数设计仿真电路模型图如图6所示，用电流探针测量的未通过同轴传输线的脉冲电流波形及频谱图如图7所示。
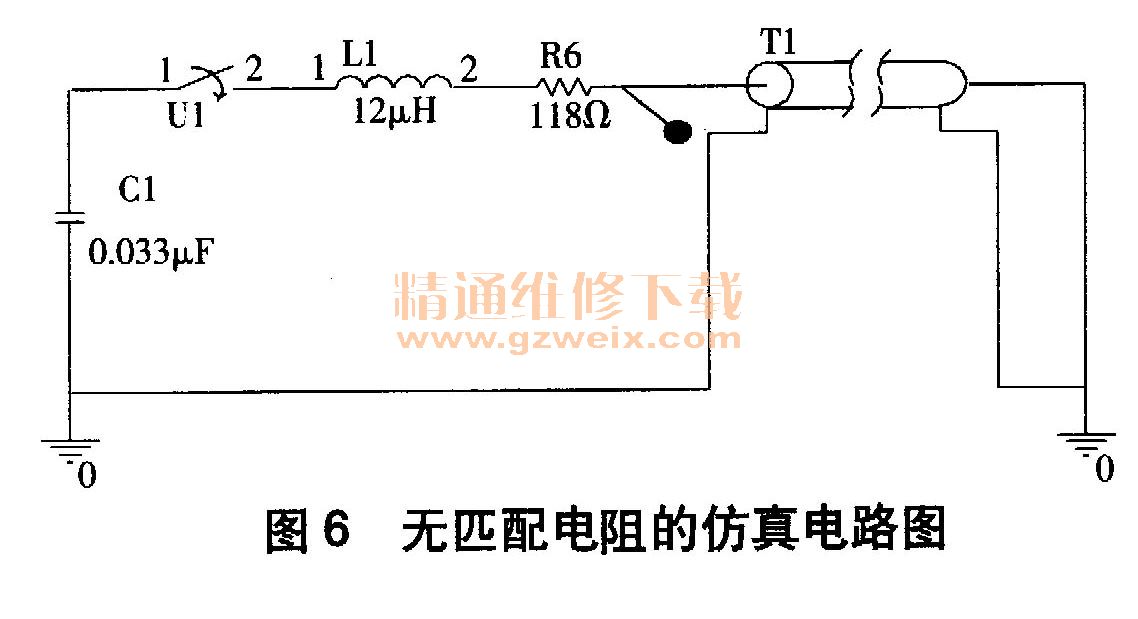
图7（a）中，脉冲电流波的VFTC现象贯穿试验全过程，且电流值越大振荡越剧烈。其原因主要是在相同反射系数与折射系数的情况下，幅值越高则对应的折反射幅值越高。该脉冲电流波形与图2（a）的差别很大，说明这两种脉冲电流的振荡机理不同。由此进一步论证，图2（a）的脉冲电流波前VFTC振荡不是同轴传输线波阻抗不匹配引起暂态行波折反射导致的。
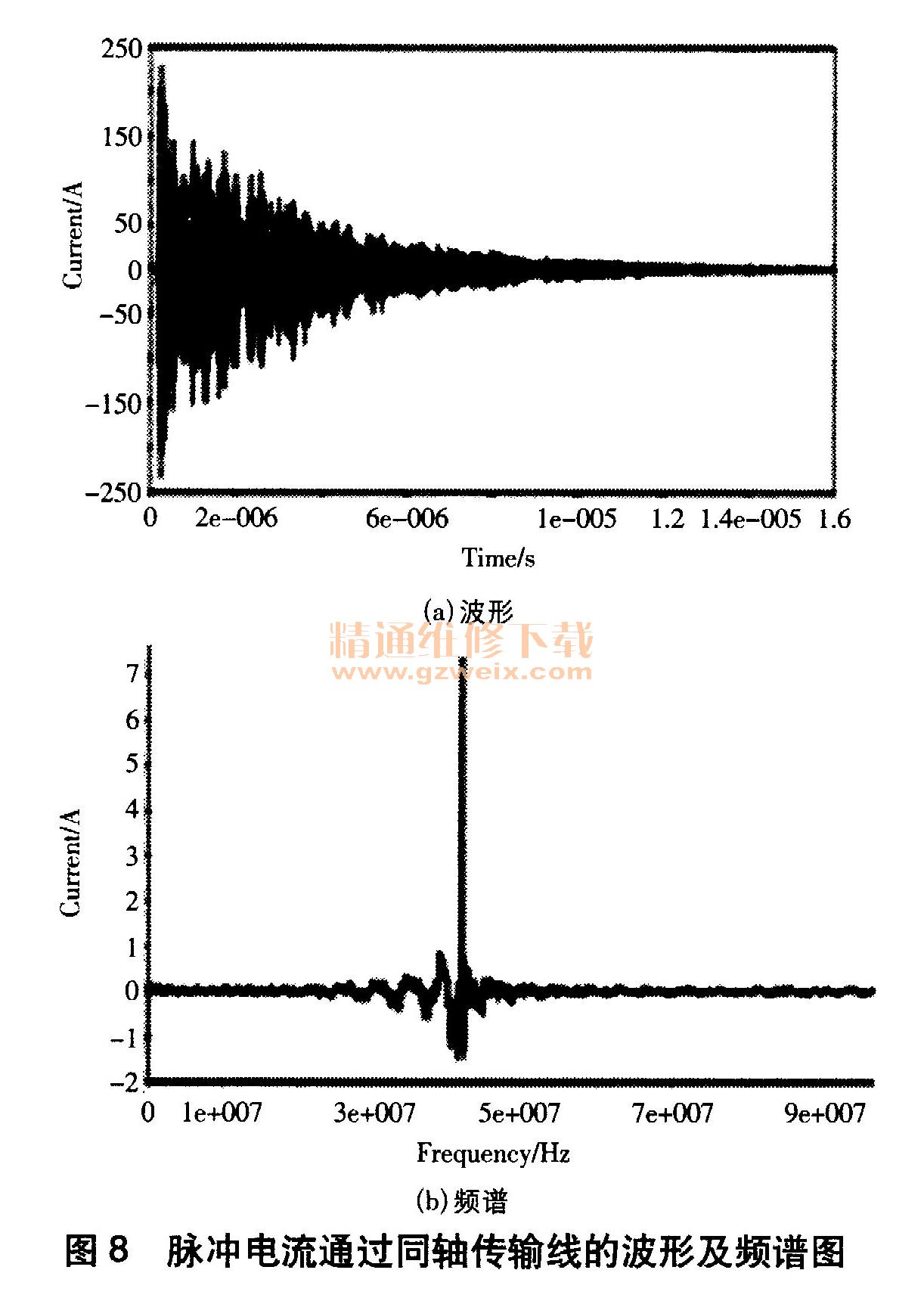
由图7（b）可知，脉冲电流波的频率是由低于5MHz和42MHz两部分构成，其余部分幅值较小可忽略不计。对比图2（b）和图7（b）发现，两者的频率构成基本一致，说明两者波形在本质上是一致的，均为实际的脉冲电流波形。由此进一步说明42MHz频率是图7（b）脉冲电流波产生振荡的主要原因，而不是构成波前VFTC的主要原因。根据参考文献巨14］可知，当传输线末端不加匹配阻抗时将导致波在波阻抗不相等处引起暂态行波折反射现象，与图7（b）波形的振荡现象相对应。
在仿真过程中还发现，脉冲电流通过同轴传输线与未通过同轴传输线所测得的脉冲电流波形存在巨大的差异。脉冲电流通过同轴传输线测得的脉冲电流波形及频谱如图8所示。
