摘要：本文利用ANSYS软件对旋转式磁保持继电器进行建模及网格划分，对磁保持继电器电磁系统的静态特性进行了仿真，计算出了静态的电磁力矩和磁链，绘制出力矩特性曲线，得出磁通密度矢量图。该仿真方法快速准确地验证了继电器电磁系统的合理性，为继电器的优化设计提供了有效手段。

    0 引言
    磁保持继电器又称磁闭锁电器或脉冲继电器，具有低功耗、耐冲击、高灵敏度、较快的动作速度以及良好的抗震动性等优点，最初被主要应用于军工、航天飞行器和卫星等重要行业，后来随着经济的发展，磁保持继电器开始广泛应用于电力行业。电磁机构作为磁保持继电器的重要组成部分，为整个继电器提供力矩和磁链，它的参数是否合理直接决定了继电器能否正常工作，因此对电磁系统的计算是十分必要的。
    分析电磁系统传统的方法是磁路计算，以前己经有很多学者利用磁路计算分析电磁系统，这种传统的计算方法过程复杂，要利用网络阻抗的方法进行磁路的计算，首先得出气息磁导，不仅计算方法十分复杂，计算十分困难，而且误差很大，这种方法适合理论分析，不适合实际的计算，在大型计算软件出现之前一直使用此方法，效率很低，结果精确度也很差。后来一些学者虽然用到ANSYS有限元分析软件计算磁保持继电器的电磁系统，但是计算的是电磁吸力，旋转式的磁保持继电器用吸力进行分析会有一定的误差，应该计算其力矩要更为精确些。当今时代，ANSYS有限元分析计算在电磁系统应用越来越广泛，越来越受到人们的重视。
    文中利用ANSYS有限元分析软件对某型号的旋转式磁保持继电器进行了电磁系统的计算，得出了在不加电流时的力矩特性曲线和施加电流时的合力矩的特性曲线，可以验证磁保持继电器的电磁系统设计是否合理。

    1 有限元仿真的分析
    1.1建立电磁系统的模型
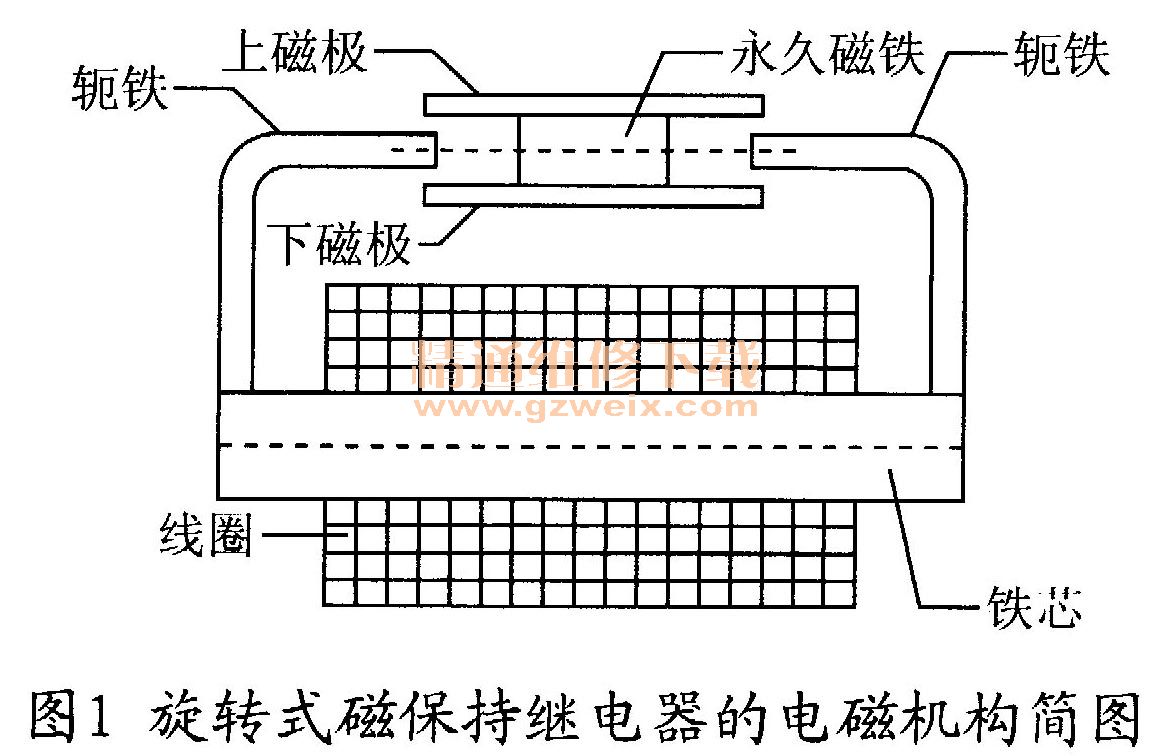
    图1是该磁保持继电器的电磁机构简图，其结构包括衔铁组件（包括永久磁铁和磁极片）、扼铁、铁芯和线圈。它通过扼铁与磁极片之间的工作气隙和衔铁组件，可以将电磁能转换为机械能，从而带动整个接触机构工作。磁保持继电器的铁芯与扼铁牢固结合，均采用高导磁的磁材料。磁保持继电器的工作原理很简单，当线圈中通以一定方向的电流脉冲时，在电磁机构衔铁组件的两个磁极间的磁场与永久磁铁的磁场方向相同，二者相互叠加产生的作用力使衔铁组件发生旋转。当电流消失时，由于永久磁铁的作用依然存在，使得衔铁组件仍旧保持在这个位置，此时称为磁保持继电器的闭合状态。同理，当线圈中通以反向电流脉冲时，两个磁极间会有与永久磁铁方向相反的磁场，并克服永久磁场的作用使得衔铁组件反向旋转。电流消失时，在永久磁铁作用下，衔铁组件继续保持在该位置，此时称为磁保持继电器的断开状态，这就是磁保持继电器的双稳态。

    在ANSYS软件中建立的电磁机构模型里面包含了永久磁铁和磁极片、扼铁、铁芯，因为此旋转式磁保持继电器具有对称性，因此可以建一半模型，然后计算的时候数据乘以2即可，这样可以在划分网格的时候节约时间，缩短总的计算时间，提高效率。
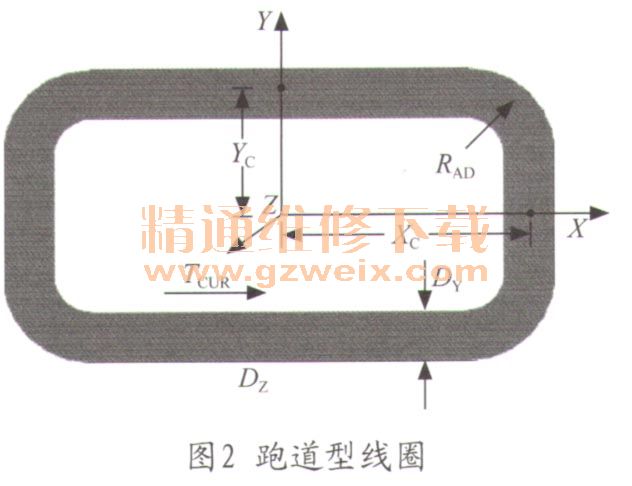
    线圈以外的模型建完后，就要施加线圈来给电磁系统励磁，对于该单相旋转式磁保持继电器，只需对它加载电流激励即可，而电流要施加在线圈上，可以用SOURC36单元通过宏 RACE建立电流型的“跑道”线圈。虽然模型建立了一半，但建立的线圈仍然是以一个完整的整体，不是以二分之一。跑道型线圈的外形及各参数的含义如图2所示。其中从和Xc是用来定位的，是从中心位置到线圈上面轴线和侧面轴线的距离，确定了线圈的位置，RAD表示拐角处拐角圆的半径，是从圆心到小圆弧和大圆弧中间圆弧的距离，Dy表示线圈的厚度，DZ表示线圈的长度，也就是外部铁芯的长度，TCUR表示磁动势，也就是线圈匝数N与线圈中所通电流I的乘积。

     1.2建立空气场并赋予材料属性
    考虑到模型周围会有一定的漏磁现象，所以在划分网格前需要在模型外面建立空气层，空气的相对磁导率为1.0。磁钢是永久磁铁，为铭铁氧体，牌号是Y30Bh，相对磁导率1.4265。金属材料为电工纯铁（D T4E ），由于D T4E是非线性的铁磁材料，在定义B-H曲线时应该在拐点的地方多选取一些点，否则会增大一误差，绘制的B-H曲线如图3所示。由图像可以看出，电工纯铁在1.8T时基本趋于饱和。

     1.3网络划分
    给模型赋予材料属性后，下一步就是网络划分，将每个模块划分为小单元，这一步是很重要的，网络划分的越细致，结果就越来越接近实际值，精确度越高，不过划分的越细，时间越长，效率会降低，因此划分的时候要注意，选择合适的精度即可，对于关键的部分网络划分要细一些，对于其他部分划分的大一些或者自由划分即可，对于某些规则的单元进行规则划分。跑道线圈是建立的虚拟电流源，因此不需要对其进行网络划分。文中划分单元类型选择四面体（3D），对扼铁上圆孔与铁芯之间的气隙、扼铁片与铁芯之间的气隙、磁钢、磁极以及部分扼铁进行规则划分，其余空气层、铁芯、辘铁剩余部分进行自由划分，同时也要适当控制其尺寸，保证划分结果中既不会有畸形单元也不会浪费计算资源或消耗过长的时间。图4是网格划分后的整体模型。

    1．4施加边界条件
    网络划分完成之后，就该添加边界条件。在电磁系统的求解问题中有很多的边界条件，通常给定的边值条件有三种类型，因此分别对应了三种边值问题。
    1）第一类边界条件：给定边界上的电位值，也称为狄利克雷边界条件。一般与场源相连的导体其电位为常数且等于外加电源的电压，这就属于第一类边界条件。该边界条件与泛定方程一起构成第一类边值问题。
    2）第二类边界条件：给定边界上电位函数的法向导数值，也称为诺依曼边界条件。该边界条件与泛定方程一起构成第二类边值问题。
    3）第三类边值问题：部分边界上给定电位函数值，部分边界给定其法向导数，即前面两种边界条件的线性组合，也称为柯西边界条件。该边界条件与泛定方程一起构成第三类边值问题，或者称为混合边值问题。
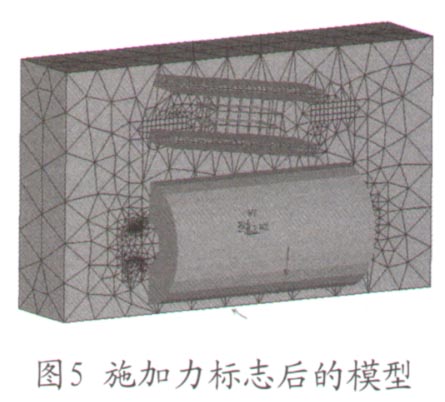
    文中用到的边界条件是系统默认的边界条件，也就是磁力线平行的条件。要计算电磁力矩，需要施加力标志，这就需要用到ANSYS中的宏FMAGSUM、它以表格的形式对作用在物体上的Maxwell和虚功力求和，前提是该物体必须被定义为一个单元组件。可以用CM命令将衔铁组件定义成一个组件，对其重新命名，然后用宏FMAGBC施加上力标志。
    施加力标志后的模型如图5所示，深色部分表示施加力标志的衔铁组件的部分，突出的圆柱部分是建立的跑道线圈，外围的长方体是建立的空气场。

[1] [2]  下一页