引 言

　　随着虚拟仪器的功能和性能被不断地提高，在许多应用中已成为传统仪器的主要替代方式。

　　本文以水循环系统为研究对象，针对水循环的温度，在比较研究不同控制策略的基础上，建立精确的数学模型，对水循环温度控制进行了研究。通过数据采集卡对温度信号进行实时采集，并由软件平台对采集的信号进行分析，然后用数学模型控制算法处理输出，以使当前温度逼近设定值，从而达到温控目的，最后将采集数据保存记录，以备日后读取分析。利用虚拟仪器的巨大优越性改善水循环温度的控制品质，提高控制效果。
 

　　1 水循环温度控制系统数学模型的建立

　　1.1 水循环温控系统介绍

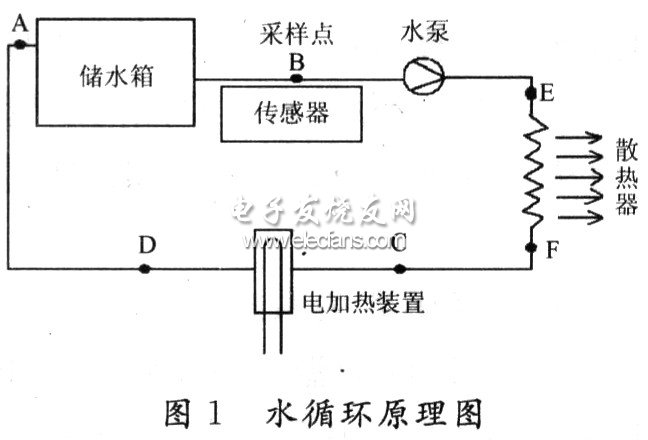
　　水循环温控系统由储水箱、水泵、传感器、散热器和电加热装置组成，水循环原理图如图1所示。由于本系统对温度要求较高，要保证水管环境温度保持在20℃，故需建立合理的数学模型及控制算法，将温度传感器PT100采样性能通过散热器及电加热器的动态温度值模拟出来，最终达到高精度控制温度的作用。

　　1.2 水循环温控系统数学模型的建立

　　水循环温控系统各个部分的温度因管道、散热装置和加热装置的原因会产生很大的变化。为了表达清楚达到预想的结果，就需要建立正确的数学模型。本设计根据实际情况，选择了几个特殊的点来建立模型。如图1所示，A，B，C，D，E，F六个点的温度，将引起变化的原因全部考虑进去，列出函数关系式，然后借助Lab—VIEW编程，由程序控制温度。

　　(1)B点的温度函数关系式

　　B点为采样点，B点的温度跟A点的温度因中间隔水箱会有一个延时K1，取在A点第N个采样值经过K1延时之后的平均值为B点的温度，它的温度函数关系为：

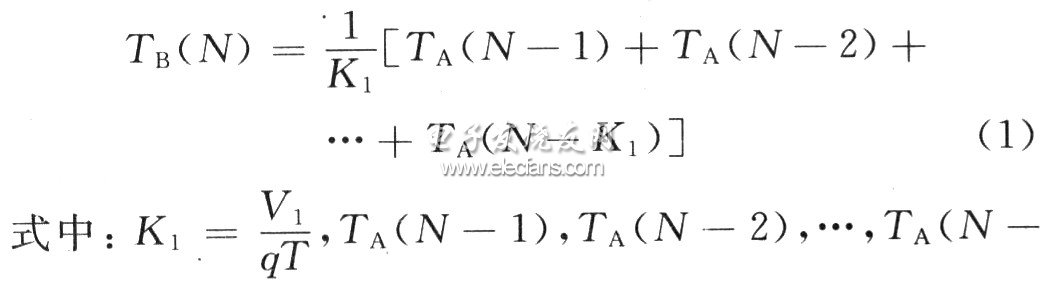
　　K1)分别为A点第N-1，N-2，…，N-K1个采样时的温度值;V1为水箱的容积，V1=5 L;q为泵流量，q=0.083 L/s;T为采样周期，T=1 s;K1：为注满水箱需要的时间，即延时周期，通过计算K1=60 s。

　　(2)A点的温度函数关系式

　　A点的温度与D点的温度因水管而有个延时，故A点的温度函数关系如式(2)所示：

　　为D点第N-K3个采样点的温度;V3为D点到A点水管的容积，V3=0.5 L;K3为从D点到A点的延时周期，通过计算K3=6 s。

　　(3)D点的温度函数值

　　D点的温度与C点温度相比，不仅仅是水管的散失而延时，还与电加热装置有关，函数关系如式(3)所示：

　　为C点第N-K2个采样点的温度;P为电加热器的功率，P=1 kW;C为水的比热容，C=4.18 kJ/kg·℃;△T为电热前后的温度变化，通过计算△T=3℃;P'为采样占控比，通过验证P'=1或0;V2为C点与D点间水管的容积，V2=1 L;K2为从C点到D点的延时周期，通过计算K2=6 s。

[1] [2] [3]  下一页