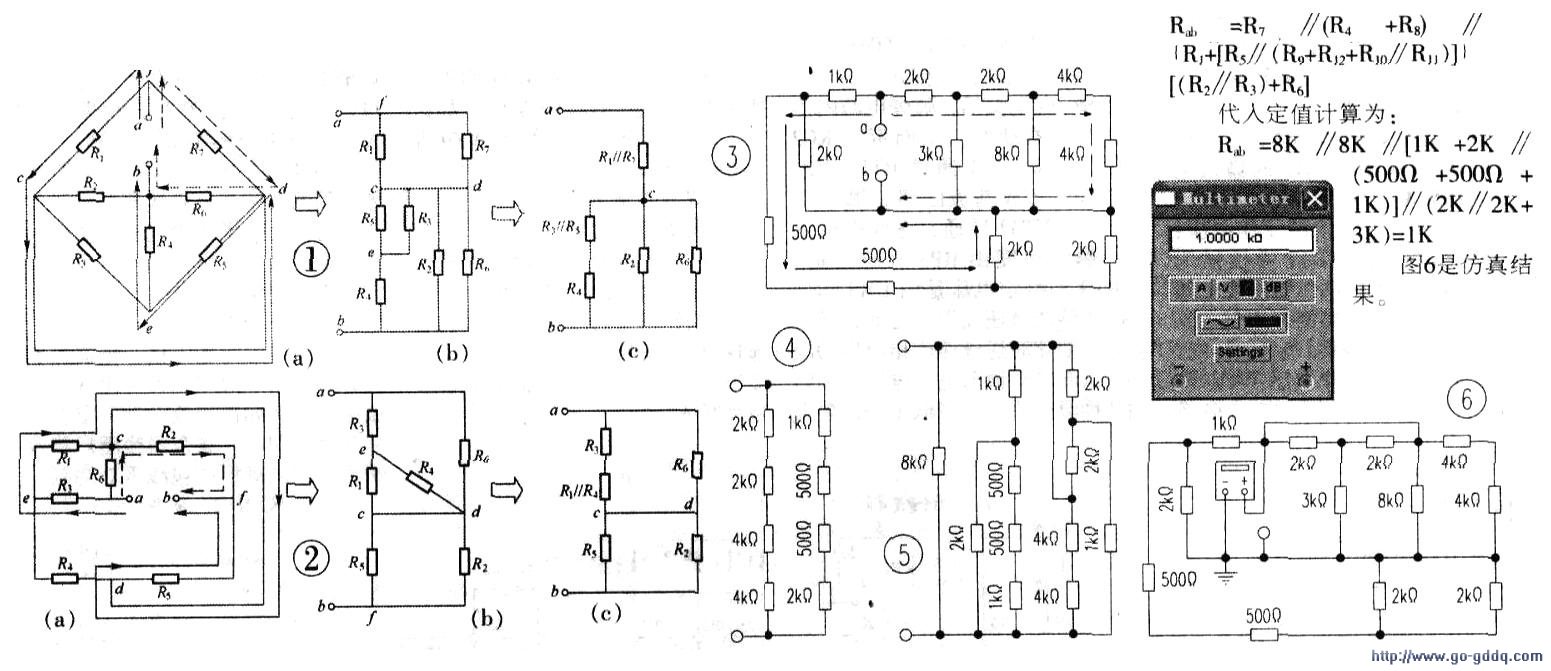
实际电路中的外负载，常常出现难以直观地判断串并联关系的复杂情况，如图1(a)所示，这类问题的分析需要先求取该电路的等效电阻来化繁为简，等效电阻的求解技术性较难，要求有更深的理论支持，在职业教育中不宜采用。如果结构中不包含△-Y连接，推荐一种实用的方法—-独立支路法定义：把不重复经过同一电阻而能使电流从正极流回负极的支路称为独立支路。

　　作独立支路的方法是：在不剩余无阻导线的前提下让支路包含尽可能多的电阻，从而使独立支路的数量最少。无法包含在独立支路中的剩余电阻，由其两端在电路中的位置决定它在新电路中的连接关系。

　　把上述方法归纳为以下两条原则：

　　原则一：第一条独立支路在不重复经过同一电阻的条件下，应该包括尽量多的电阻。．原则二：涉及三个电阻以上的无阻导线应优先画在第一条独立支路中。

　　下面举例说明这种方法的使用。

　　【例1】如图1(a)所示，已知Ri=6Ω.R2=R3=1OΩ.R4=4Ω,R5=40Ω,R6=15Ω，R7=12Ω．求a、b端口处的等效电阻。

　　使用“独立支路法”解答本题时．具体做法是：由a，b两端引入假想电流I，图1(a)中I由a点流人，第一条独立支路在c点时，遵循“原则二”三条可能路径只能选择流向d点，遵循“原则一”．经过d点后必须通过R，和R4由b点流出，从而构成图1(b)中的R．、Rs和R4三者串联的第一支路。第二条独立支路如图1(a)中的虚线所示，即图1(b)中R7和R6的串联支路。

　　两条支路包括了5个电阻，还有R3、R2无法形成独立支路，只能根据它们在电路中的连接关系将它们画在新的电路图中。

　　注意：本题还有一个容易忽略的问题，即两条独立支路之间的关系连线，由于c、d两点之间无阻导线的存在，在图1(b)中应注意补画一条短线，以准确地完成等效电路。

　　解：本题以a点为起点'b为终点，逐次整理出等效电路图，如图1(c)所示。

　　R5与R3并联再与R4串联，其等

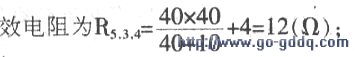
　　R2与R6并联再与R5.3.4并联后的等效电阻R2.6(5.3.4)=4(Ω)；则a、b端口处的等效电阻为这两个电阻之和，即Rah=R1.7+R2.6(5.3.4)=4+4=8(Ω)。

　　[例2]如图2(a)所示，已知Ri=20Ω.R2=12Ω,R3=1OΩ,.R4=5Ω,R,=8Ω．R6-14Ω．求a、b端口处的等效电阻。

　　解：由独立支路法可知，将原电路分成两条独立支路：一条是由aecdf到b．另一条是由acf到，R4由其两端在电路中的位置决定，等效电路如图2中的(b)、(c)所示。

　　Rab,=[(R3+R1//R4) //R6]+(R5//R2)=ll.8(Ω)

　　[例3]把图8电路应用“独立支路法”分析如下：

　　如图3所示（为提高兴趣、方便验证，给各个电阻赋了定值）。求B、b端口处的等效电阻。

　　在图3中引入两条“独立支路”（如图3中实、虚线所示），得到图4所示部分简化电路。然后在图4中舔加上一条短线和四个剩余电阻(原图中的R5、R6、R7及Rll)，即得到圈5等效电路。注意，在圃虚线所示独立支路时．没有采用上述的原则二，原因是这条”无阻导线”所涉及的电阻只有两只．不需要先行解决。

　　根据图5．可以很方便地得到原文的结果，即：