二、模型建立
      以宝骏560五速变速器为例，对其进行键合图建模阎。工作简图如图1所示。将I,II挡主动齿轮与输入轴固连，并利用滚针轴承在输入轴上空套III、IV挡主动齿轮，而输入轴与V挡之间的连接采用压配合；采用花键紧配合的方式连接输出轴和III、IV挡从动齿轮，并利用滚针轴承将剩余的挡的从动齿轮空套在输出轴上回。采用花键配合的方式连接轴与每个挡的同步器（出于直观，未在图中画出同步器冲。I到V挡的主动齿轮如图1中的数字1～5所示；I到V挡的被动齿轮如图1中的数字6～10所示；倒挡的主动齿轮和被动齿轮分别如图1中的“倒”和“倒1”所示。

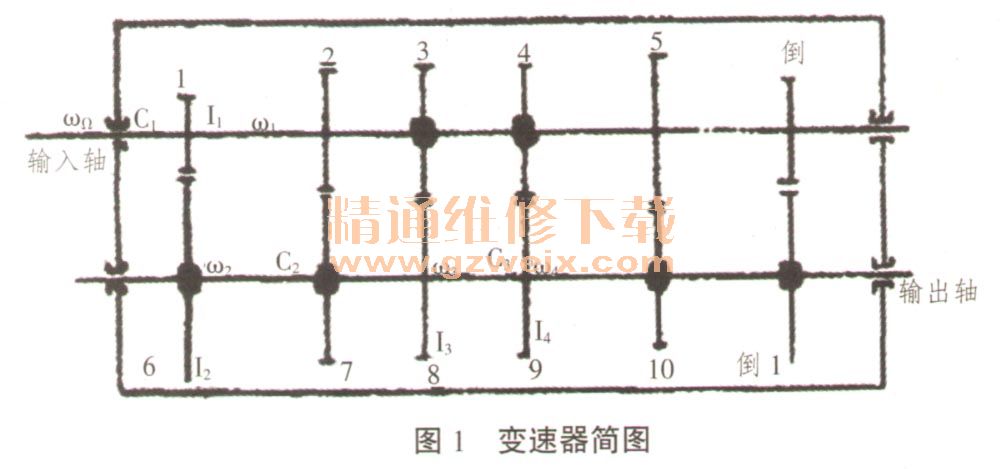
    如果不考虑变速器的功率损失，将其置于I挡的位置，空套于轴上的齿轮不会对轴有影响；而与轴制成一体的齿轮因为与轴同步旋转，类似于惯性飞轮，所以就会影响轴的转速及其弹性特性。系统的弹性与惯性用当量弹性与惯性来代替，用数字1,6,8和9表示的齿轮的转动惯量分别用惯性元件11到14来表示，而每段轴的弹性特性及其转速分别用容性元件C和。表示。通过绝对速度，对该变速器进行键合图建模，对键合图中的键进行命名，并明确每个键的因果关系及功率流向，从而获得如图2所示的系统增广键合图。

    三、状态方程
    在变速器动态分析的过程中，要求解出3种数学模型之一，即状态方程、传递函数或方块图，而利用键合图能非常容易地得到这些数学模型。本文研究了变速器状态方程的求解过程。在图2中，C2、I4、I7、C9、I11、C13和I15都是储能键图元，其中除了I4变现微分因果关系之外，其余都表现出积分因果关系。而q2、p4、p7、C9、I11、C13和I15分别为储能键图元对应的能变量。
    公共势和流结点分别用“0”和“1”表示，按照变速器的特性，得到f4=f6=if6=if7。
    对应惯性元件L1得到P=e f=P/1；而对于容性元件C，得到P=f，e =q/C。故p4=Il4i7-1p7。
    所以p4不是状态变量，因为其不是独立变量。故在图2中q2、p7、q9
    p11、Q13和P1。为状态变量。F1和E16为
    系统的输入。
          根据键合图计算状态方程，结果
      为：

    状态方程中变量的下标为图2中键的标号，而，I与C作为系统的参数，若系统一定则数值就一定。
    利用变速器的状态方程能获得其幅频特性，最后再进行仿真研究。基于以上方法，不仅能够对汽车的发动机、车身、半轴和离合器等进行建模，还能够建立汽车的整车键合图。

    四、结论
      1．根据键合图能够解出变速器不同的数学模型，并基于数学模型能够进行动力学仿真以及分析系统动力特性。
    2.键合图完全能够应用于汽车传动系统各组件的建模。
 

上一页  [1] [2]