摘要：本文针对孤网变频系统中电量频率跟踪及计算的要求，提出一种孤网变频系统中电量频率跟踪方法。该方法基于傅里叶变换，提取电流电压信号中的电量待测信号的基波分量，通过过零点检测方法确定电量待测信号的基波分量的过零点，并记录每个过零点间的采样点数，利用频率计算公式得到待测信号的频率。结果表明，该方法具有较高的鲁棒性，跟踪频率范围较宽，在假设频率为50Hz时，信号频率在20～100Hz均能正常跟踪，同时算法实现简单，测量精度达到要求，且具有较高的抗噪声干扰能力。

    某新型电气节能系统孤网运行时，通过调整频率来改变风机及泵类负荷的转速，以达到节能降耗的目的。该系统为不接地系统，孤网运行时频率变化范围为35～50Hz。目前，国内现有小电流接地检测装置在技术上均不能满足非工频系统的要求。为了保证该系统的安全运行，解决变频下发生单相接地故障时无法准确判定接地位置的问题，需要研究孤网变频系统电量频率跟踪方法，进行接地电流计算。
    目前，频率跟踪算法中过零点检测和计算周波数是最为简单和常见的方法。另外，离线傅里叶变换、最小二乘法及Kalman滤波是很成熟的数字信号处理技术，也可用于频率测量。但是，在频率跟踪中仍会遇到问题：噪声干扰，在实际过零点附近存在波动，出现多个假过零点，导致频率测量误差；高次谐波的影响，系统信号中往往含有高次谐波，导致过零点与基波过零点出现偏差，影响频率测量。

    1 电量频率跟踪方法原理
    本文提出的孤网变频系统电量频率跟踪方法的主要原理包括基波分量提取、过零点检测和频率计算。
    1.1基波分量提取
    设初始信号为x（t），则有：
    x（t）＝Ccos（ωt＋ψ）＋R（t）    （1）式中，C为基波分量幅值；ω为基波分量角速度；ψ为初相位；R（t）为高次谐波和均值为零的白噪声信号组成。
    若基波分量角速度ω未知，假设其为ωa，则得到傅里叶系数X为：

    A＋Jb    （2）
式中，A、B分别为傅里叶变换的正、余弦分量；。。为傅里叶系数中的角频率；m为假设频率中一个周期的采样点数；Ta＝2π/ωa；xn表示第n个采样点。
    假设采集系统的采样率fs=m/Ta=1/Ts （Ts为采样间隔），则在离散傅里叶序列中，基波分量的频率可用采样间隔和基波分量一个周期内的采样点表示，即1/（采样间隔X采样点数）。待测信号的基波分量cosine和sine，即A和B，是时间的周期函数，且A（t）和B（t）是待测信号频率f的正交周期函数。
    cosine基波分量表达式为：

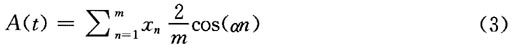
式中，n为采样点位置；m为一个周期内的采样点数；xn是对应的采样点值；a为ωaTa/m，对于余弦基波分量，
ωa Ta＝2πfaTa。
    1.2过零点检测
    过零点，如从正半轴到负半轴，指上个周期中最后一个采样点为正值Ap，下个周期第一个采样点为负值An，如图1所示。在过零点区域，cosine函数用线性函数表示为：



式（4）可变形为：

    当基波分量经过过零点时，从正半周到负半周，P表示下个周期的第一个采样点；在下个过零点处，从负半轴到正半轴，K表示前个周期的最后一个点，P表示下个周期的第一个点，所有介于A，和A，间的采用点等于1，同一时刻P＋K的值永远等于1，其中P< 1，K< 1。
    1.3频率计算
    根据过零点检测得到的一个周期内的采样点个数，通过统计M个周期内的平均样本数，计算基波分量的频率。MA表示M个周期的采样点数，每个周期内采样点数为：

式中，fa为假设基波分量的频率；m为基波分量一个周期内的采样点数。
    根据式（8），计算基波信号的频率f，即得到待测信号的频率。

[1] [2]  下一页