永磁直流电动机用永磁体取代了定子上的励磁，但是仍然需要电刷换向器结构。电刷换向器结构是普通直流电动机的特征和标志，它使转子上的导体在经过磁场的换向点的时候自动改变电流方向，导致定子同一磁极下导体的电流方向不变，转子的磁场始终与定子的磁场垂直，从而获得最大的也是稳定的转矩，保证了直流电动机优良的控制性能。

    电刷换向器结构也是普通直流电动机的先天性的弱点，人们一直在探讨利用现代电子技术，实现既能取消电刷，又能达到直流电动机优良控制性能的方案。这些方案中最著名的就是交流电动机的矢量控制，而无刷电动机也是在这个方向上发展所取得的成果。

   这个发展的特点是转予采用恒定磁场，而将普通电动机中的电枢电路从转子转移到定子上去，这种励磁和电枢位置的互换对两者之间的相对运动没有影响，但是却避免了电刷换向器结构。如果转子由外部直流电源励磁，那么转子还需要电刷和滑环，还只能称为无换向器电机。如果采用永磁材料制作转子，那么就可称之为无刷电动机。

    虽然感应电动机和后面将介绍的步进电动机也是无刷的，然而无刷电动机则是专指这样一些特种电动机，这些电动机的设计目的是具备与有刷直流电动机类似的性能，但是却没有电刷换向器结构所强加的限制。

    无刷电动机具有基本相同的本体结构，另一个重要的共同点是运行时需要通过检测转子的位置来确定驱动电源的频率，因此无刷电动机在本质上属于自控变频同步电动机。无刷电动机因其电枢绕组驱动电流形状的不同而分为两种类型：一种是方波永磁同步电动机，其电枢驱动电流为方波（梯形波通常被称为无刷直流电动机；另一种是正弦波永磁同步电动机，其电枢驱动电流为正弦波，常称为无刷同步电动机。

　　无刷直流电动机的基本原理

   首先回顾一下传统的有刷直流电动机。有刷直流电动机的转子上的电枢绕组由许多单独的线圈元件组成，一个单独的线圈元件在旋转时其输出转矩的幅度有很大的变动，实际上是按正弦规律变化的，其最大值出现在与定子磁场垂直的位置，而在换向位置时的值为零。它们不仅连接到自己的一对换向片上，而且还与其他的线圈相连，尽管电机的转矩主要由处于最大转矩位置的线圈元件提供，但是由于处于不同位置的其他线圈元件共同作用，最终产生的转矩波动很小。

    如果将这种思想移植到无刷电动机的设计中去，将许多线圈元件平均分布在定子上，然后采用电子线路模拟电刷换向器结构的功能，其结果将是不仅控制电路非常复杂，而且每一个线圈元件都需要自己的单独的驱动电路。这一点显然难以满足。因此为了实现无刷化，必须作出适当的折衷和妥协。

   　 图11.6为一个二极三相无刷直流电动机的结构。

    无刷电动机具有少则2组、多至5组的线圈绕组，称之为相线圈或相绕组，图11.6中的二极三相无刷直流电动机的三个相绕组A1-A2、B1-B2和C1-C2分别绕在相对的两个磁极上。三个绕组可按三线Y接法、四线Y接法和三线△接法连接。图11.6为目前主要应用的三线Y接法。

 　 在理想的状态下，定子和转子的两个磁场最好是保持互相垂直，这样才能产生与有刷直流电动机相近的性能。但是无刷电动机定子相当于只有三个线圈和三个换向片的直流电动机电枢绕组，在定子的三相绕组由直流供电的条件下，这一点显然是做不到的。

  　无刷直流电动机中转子磁势与定子磁势之间的夹角称为转矩角。定子磁场换相电路的设计思想是使转矩角的平均值是90°。以二极三相无刷直流电动机为例，在转子旋转一周的过程中，定子磁场按60°的增量步进6次，并且设计换相逻辑使转矩角在120°～60°之间变化。就是当定子磁场进入6个位置之一的时刻，转子磁场与定子磁场的初始夹角为120°，并受定子磁场的吸引朝着夹角减小的方向旋转，当夹角达到60°的时候，定子磁场又向前移动一个位置，使夹角再次增加为120°。在转子的一个60°旋转过程中，定子磁场保持不动。

    因此在无刷电动机中，定子磁场的移动有两个特点：一是这种移动是步进的而不是连续的；二是这种步进的速度不像步进电动机取决于外部的脉冲频率，而是取决于电动机本身的转速，通过对转子位置和旋转方向的检测来实现定子绕组的换相。所以这种电动机是自同步的，没有步进电动机和同步电动机的失步问题。

    对于不同的绕组接法可采用不同的驱动电路拓扑，例如四线Y接法可采用三相半桥驱动，而三线Y和三线△接法则需要采用三相全桥驱动（图11.7）。下面以应用最广泛的三相全桥驱动的三线Y接法的无刷直流电动机为基础进行讨论。

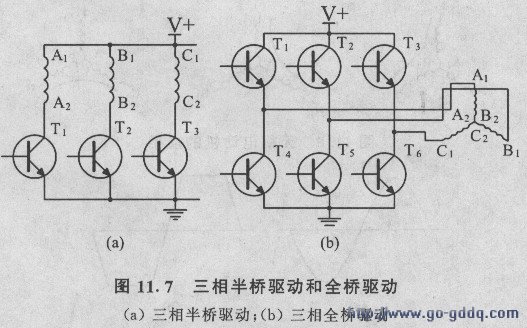
    三相桥式驱动电路在每个时刻，只有上半桥和下半桥中各一个晶体管导通，使外部直流电源接人A1、B1和C1三个接线端中的两个，使得三个绕组中的两个串联接到电源上，而第三个绕组则没有通电。与有刷直流电动机的换向对应的操作演变为无刷直流电动机绕组切换的“换相”，其换相一共有6个节拍，每个节拍代表三相绕组的一个状态，产生定子磁场的一个确定的角度。这6个节拍的顺序、导通的晶体管和绕组的接入极性如表11.1所示。前3拍的定子磁场位置如图11.8所示。如果在正向旋转状态下各拍的顺序是1-2-3-4-5-6-1的循环，那么在反转时的顺序是6-5-4-3-2-1-6的循环。

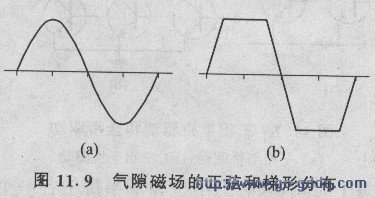
   无刷直流电动机的励磁由转子提供，而气隙磁场则是由转子磁场和定子的电枢反应共同形成。气隙磁场的波形对电枢电流、电动势和电磁转矩的影响是不言而喻的。以往的无刷直流电动机设计都是以正弦分布的气隙磁场为基础(图11.9(a))。近年来随着材料的发展和设计方法的改进，新型无刷直流电动机的气隙磁场为具有足够宽度的梯形分布(图11.9(b》，这两种情况下的转矩特性是不同的。

    电磁转矩可以认为是定子的电枢磁势和转子磁势相互作用所产生的，如果不考虑磁路的饱和和磁势的高次谐波，电磁转矩表示为T=KFaFr，其中K为常数，Fa为定子磁势，Fr为转子磁势。

    然而在气隙磁场不是均匀磁场的情况下，Fa取决于电枢电流ia，Fr取决于转矩角，这两者都不是常数。无刷直流电动机的电枢绕组具有电阻，在切割气隙磁场时会产生反电动势，这些和普通的直流电动机类似。对于三相桥式驱动的三线Y接法，电枢中同时导电的两相绕组形成当时的电枢回路。如果气隙磁场为正弦分布，则回路中的总反电动势为两相绕组中反电动势的向量和，则可得到电枢的回路方程为

式中U-电枢输入电压；
    Ra-相绕组电阻；
    ia-电枢电流；
    Ea-反电动势的幅值。
    由式(11.18)可求得电枢电流

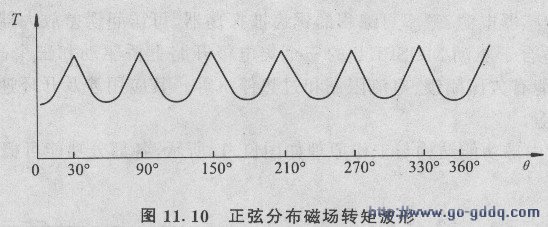
  　由式(11.20)可绘出正弦分布气隙磁场无刷直流电动机的转矩波形如图11.10所示，可以看到转矩随转角有一定程度的脉动。

    新型无刷直流电动机通过改进设计，采用如加大极靴宽度等措施使得气隙磁场分布为梯形。结合考虑三相桥式驱动的开关顺序，可以绘出三相Y接法的无刷直流电动机各相绕组中的反电动势EA.EB和Ec，电流iA、iB和IC，转矩TA. TB和Tc的波形(见图11.11)。从波形图我们可以注意到以下几点：
    (1)反电动势取决于磁场的波形，因此为相隔120°的梯形波；
    (2)各绕组导通时正处于梯形波磁场的平顶部分之下，得到的转矩为120°的方波；
    (3)理论上合成转矩丁为当时导通的两相绕组转矩的代数和，得到的电动机转矩是几乎没有波动的恒定转矩。然而实现标准的梯形波磁场是不可能的，梯形波顶不可能完全平直；此外，电枢电流在绕组间的换向也不是可以在瞬时完成的，电流波形应该近似于梯形波，因此转矩的波动总是有的，特别是在换相的时刻会出现转矩的明显波动。

    无刷直流电动机的动态特性与普通直流电动机在本质上相同，此处不再详细推导。