2．节流管管径为4mm情况下的仿真结果
    节流管管径始终保持1个数值（4mm ），节流管就会对空气弹簧与附加气室之间的空气流动产生阻碍。这样相当于空气弹簧与附加气室之间联系的紧密程度下降，在这种情况下空气弹簧气压与附加气室气压的波形将会产生差别。
    将节流管的内径变更为r=0.004m，其它参数与表1完全相同。此试验条件下，空气弹簧气压、附加气室气压变化规律如图3所示。

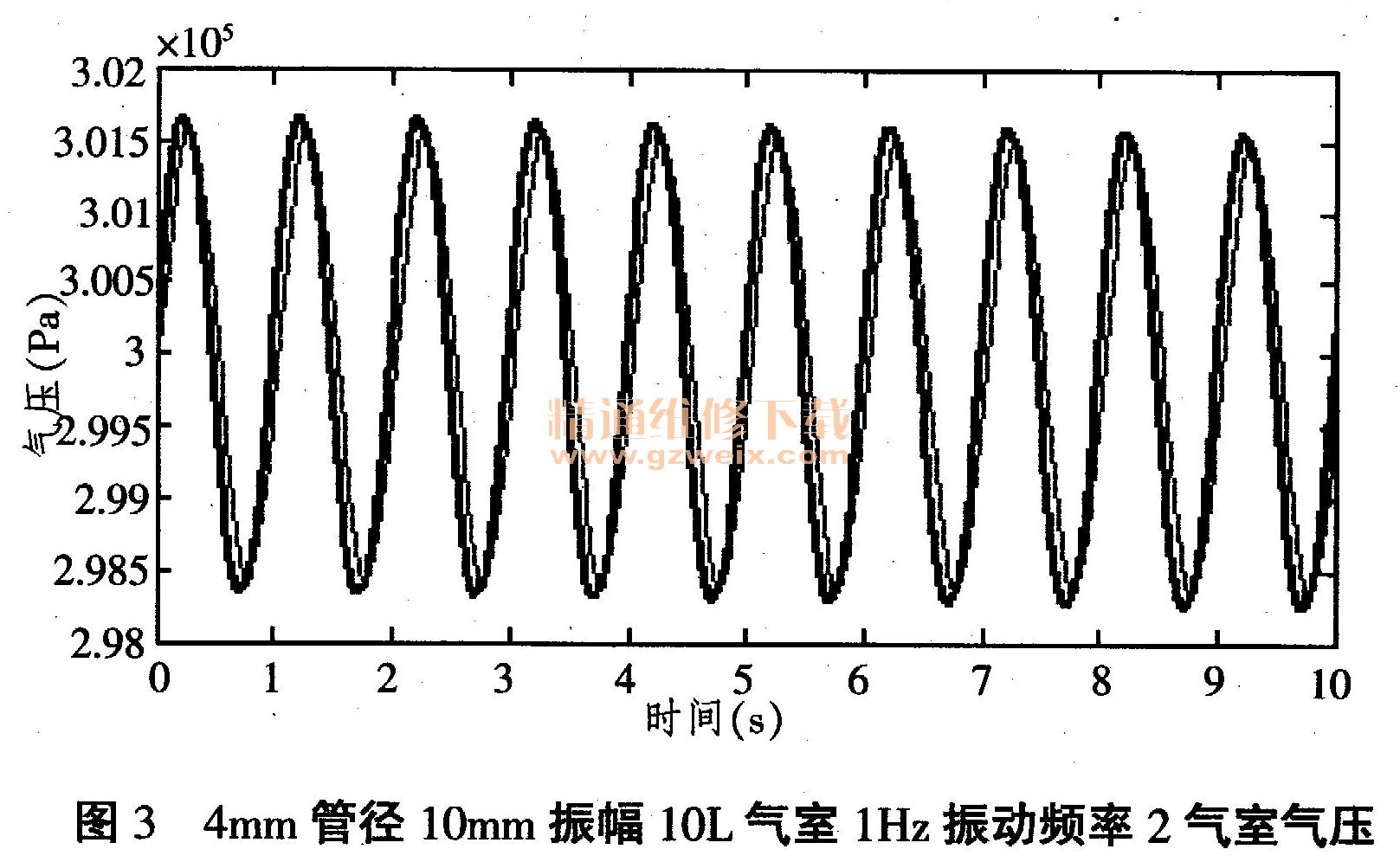
    此仿真结果表明，节流管管径下降，空气弹簧和附加气室的气压变化幅度略有变化，且2处气压在波动中产生了一定的相位差。由于此时仍处于低振幅、低频率的情况，因此2者的区别还不明显。
    此情况下空气弹簧刚度为K=5344N/m，与节流管内径为20mm的情况相比，刚度略有增加。
    下面，其它条件不变，把振幅改变为2mm，则仿真结果如图4所示。

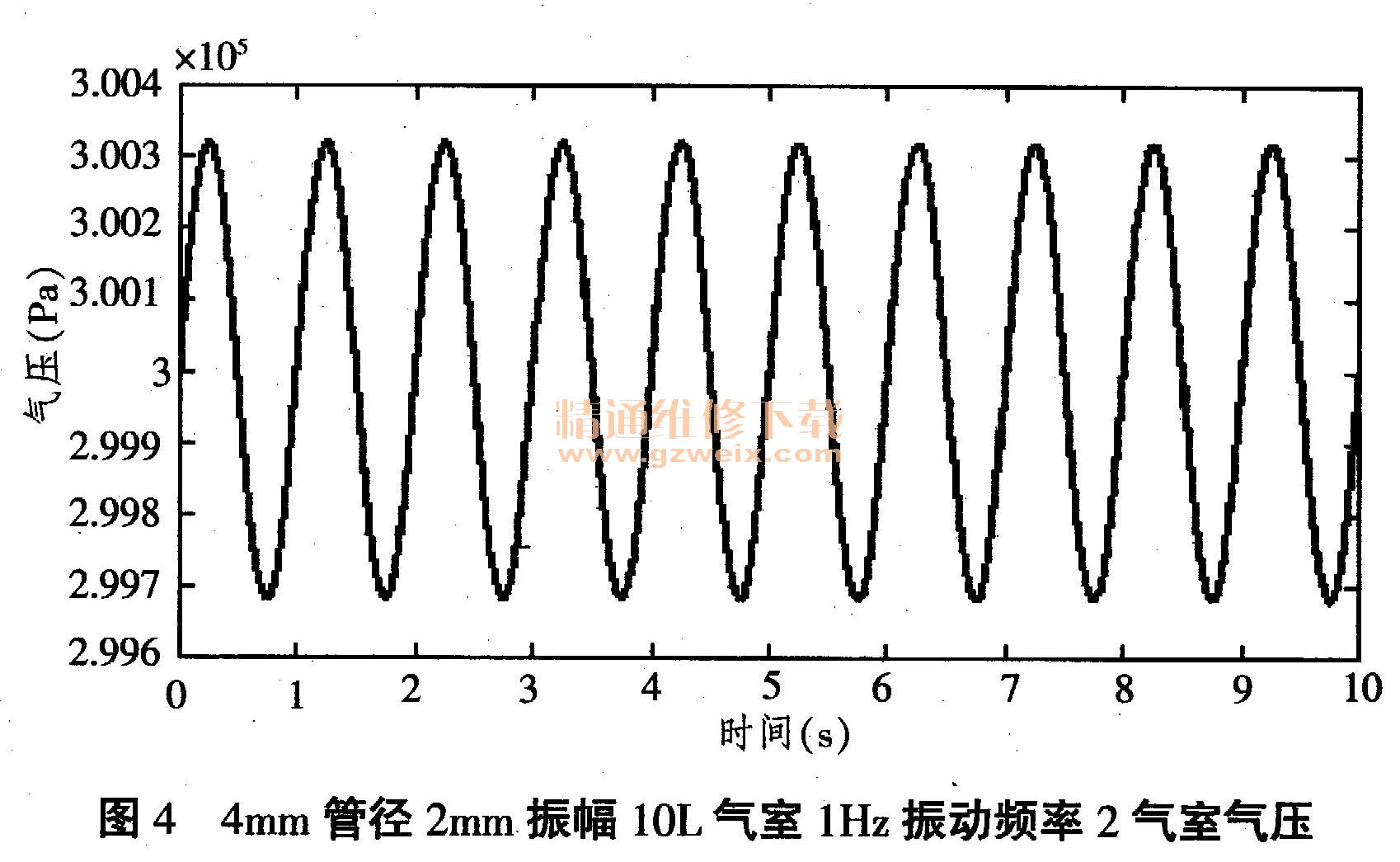
    可以看出，振幅减小，除影响2处气压的振幅，使之减小外，还使2气室的相位差减小。系统刚度下降回原来的5216N/m，说明在振幅2mm的情况下，空气流动速率较缓，4mm的管径也足以使空气在2气室自由流动。
    把振幅调回10mm，振动频率改变为5Hz，则仿真结果如图5。

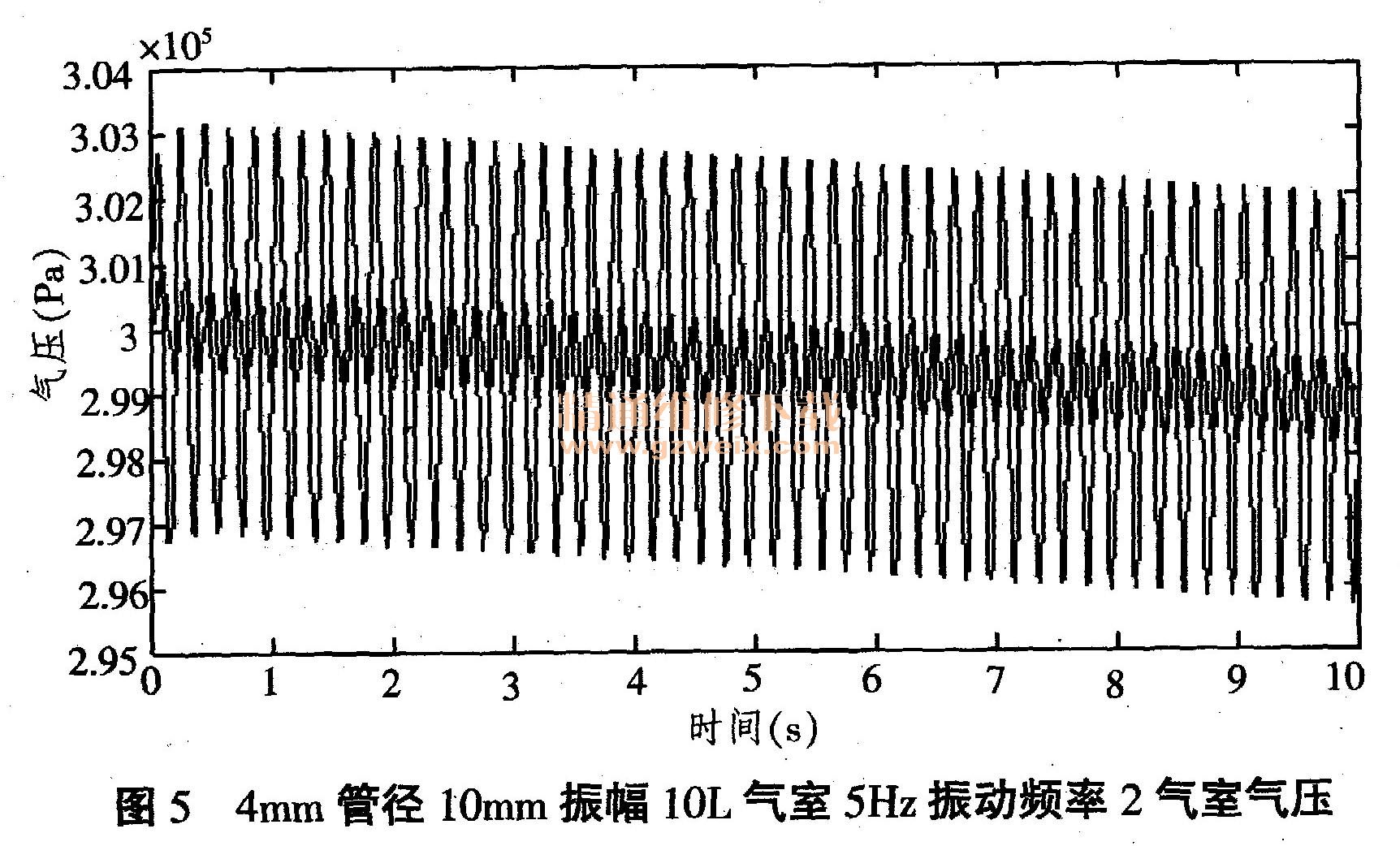
    除气压的振动频率改变外，空气弹簧的振幅明显大于附加气室，且附加气室相位滞后于空气弹簧。
    此时的系统刚度，K=10144N/m。说明在此试验条件下，空气弹簧频率升高，会提高空气弹簧刚度。
    把振动频率调回1Hz，使附加气室大小变为40L，仿真结果如图6。

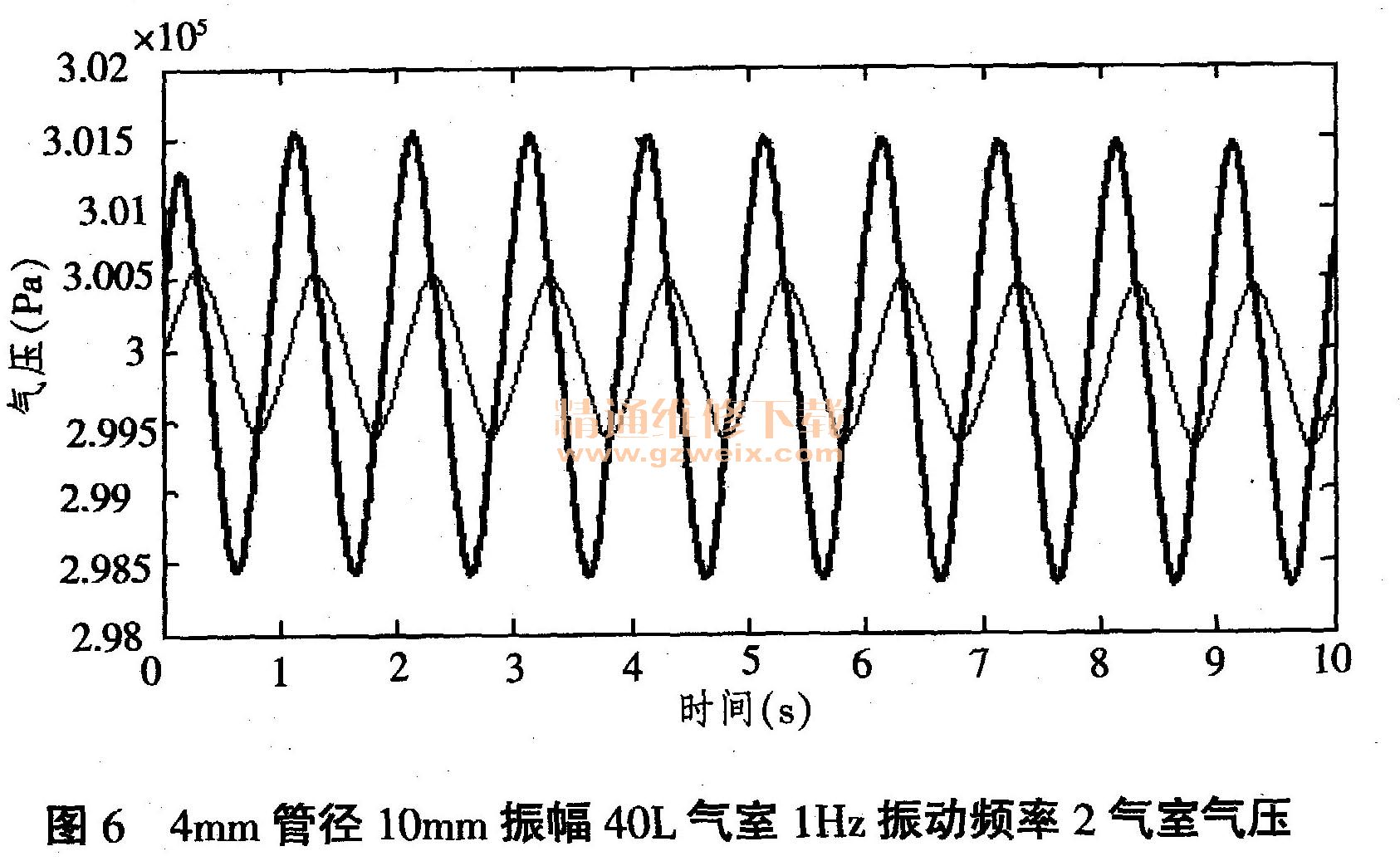
    同样，空气弹簧气压比附加气室气压的振幅更大，相位更靠前。
    经计算，此时空气弹簧的刚度下降到K=4960N/m。相对于附加气室10L的情况，刚度有所下降。但节流管管径为20mm时，附加气室从10L变到40L，导致空气弹簧刚度从K =5216N/m下降到1984N/m。而此时，节流管管径为4mm，附加气室刚度的变化为从K=5344N/m下降到K =4960N/m，相对变化幅度很小，说明在节流管管径为4mm时，附加气室体积增大对减小空气弹簧刚度的效果下降了很多。
    为研究节流管内径对系统刚度的影响，特地在1Hz，10mm振幅、40L附加气室体积的仿真条件下，让节流管内径从4mm变化到20mm，仿真计算空气弹簧—附加气室系统刚度。仿真结果如图7。

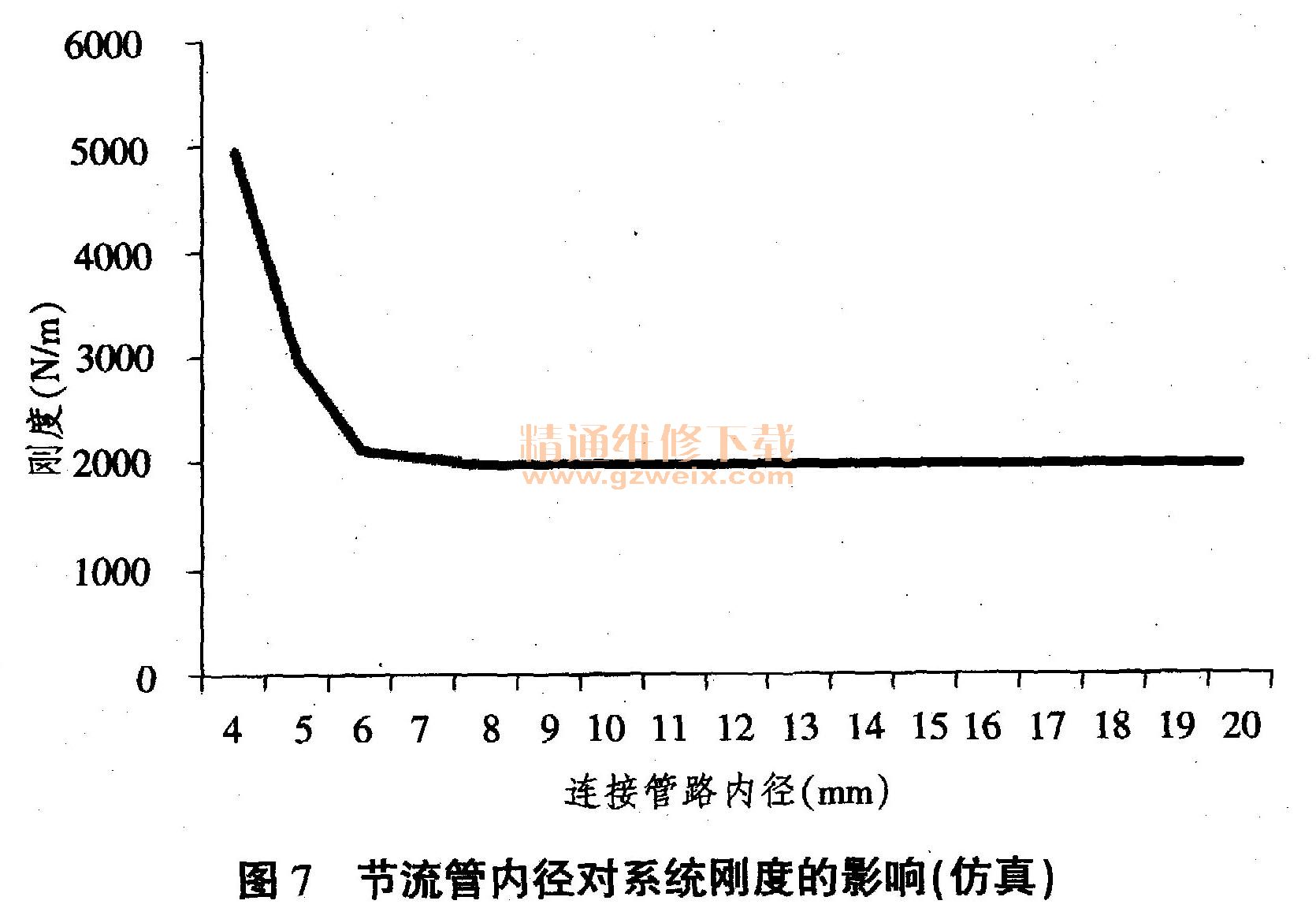
    刚度随节流管内径增加，先单调下降，继而保持稳定。并且，刚度增加的同时，伴随着附加气室与主气室气压变化的相位差增大。
    综合以上仿真结果可知：空气弹簧—附加气室系统的刚度与附加气室大小有关。在其它条件不变的条件下，系统刚度随附加气室的增大而减小。此外，节流管内径也是一个很重要的参数。节流管内径的大小决定空气弹簧与附加气室联系的紧密程度：内径越大，空气弹簧与附加气室联系越紧密，相位差越小，附加气室对刚度的降低效用越能充分发挥；内径越小，空气弹簧与附加气室联系越·不明显，相位差越大，附加气室对刚度的降低效果越不明显。在节流管内径从“足够大”（空气弹簧与附加气室的气压在仿真过程中基本不存在相位差）变化到0的过程中，空气弹簧—附加气室系统的刚度先是基本不变，然后逐渐变大。在节流管内径并不足够大的情况下，输入激励振幅或频率的提高，都会使附加气室的效果更加不明显，进一步增大空气弹簧的刚度。

    三、小结
    本文旨在对可变附加气室容积空气弹簧特性进行理论研究，主要研究手段是用MATLAB中的Simulink模块搭建仿真模型。通过研究与空气弹簧相关的流体力学及工程热力学的相关知识，并结合空气弹簧自身特性，成功推导出了在空气弹簧受到路面正弦激励情况下，空气弹簧与附加气室气体交换的过程方程。利用此方程，搭建了仿真模型，进行了仿真，分析出了变附加气室空气弹簧的一些力学特性。由仿真模型的示波器图形看出，仿真的偏差不大，可以正确反映当空气弹簧—附加气室系统的一些参数变化时，空气弹簧力学性能的变化趋势，这也为后续的试验研究奠定了基础。

上一页  [1] [2]