摘要：主要运用了有限元分析的方法来研究机械传动系统体系中的扭转振动及其效果，在此基础上经过相应数据处理与计算之后，基于灵敏度的效果评价分析来进一步对该机械设定模型进行动力学修改，最终分析出机械传动系统扭转振动频率的发生概率时空分布。

    机械传动系统在国内机械工业工程领域的应用比较广泛，如汽车制造业、航空领域以及各种大型功率性的机械机组，本文以发电风机为重点，基于有限元分析来进一步研究机械传动系统扭转振动模式。

    1 机械传动系统
    1.1传动系统的发展
    机械传动在工程应用领域主要是指利用机械方式传递动力和运动的传动，具体可将其概括为两大类，一是靠机件间的摩擦力传递动力与摩擦传动，第二种类型主要是靠主动件与从动件啮合或者是借助于中间件啮合来实现传动力的传递。当前国内自动化控制型的机械传动系统，是经历过数千年的发展历史演变而成的，在我国的西汉时期出现了齿轮传动，大家最为熟知的指南针就是充分运用了这一原理，在我国商代时期，出现了链传动，而东汉时期由张衡发明的水利天文仪器就已经使用了相当复杂化的齿轮传动系统。
    1.2我国风力发电机组设备
    风力发电机的可靠性、稳定性，关系着整个风力发电机组的整体使用寿命和相应的维护管理成本费用。在以往的针对风力发电机组等大型机械传动系统的研究、技术创新过程中，比较注重以风电齿轮箱质量和增速箱质量为研究对象，本文基于有限元分析的方法来对整个风电机械传动系统进行简化式的探索研究，通过对传动系统中扭转振动模式及其效率的研究，全面挖掘、分析其内在的动力学特性。
    我国北方某风力发电系统工程项目，其中的风力发电机组传动系统结构分布，如图1所示。C1代表的是传动链系统中第一级行星架，C2代表的是第二级行星架；其中的：1代表的是传动链系统内第一级内齿轮（固定），而：2代表的是机组传动链系统内第二级内齿轮；Sj代表的是机组传动链系统内第一级太阳轮，Sj代表的是机组传动链系统内第二级太阳轮；Pi代表的是机组传动链系统内第一级行星轮（其中，i=1、2、3）、Qj代表的是机组传动链系统内第二级行星轮（其中， 1=1，2，3）。

    选取并确定其传动链系统内几何参数数据如表1所示。

    2 风电机械传动系统中的齿轮副扭转振动模型
    如图2所示，该风力发电机组传动系统扭转振动模型可根据牛顿第二定律来进行表示，由图所示，在已知的齿轮副重合度为1-2，下面通过建立相应的运动微分方程组来进行表示：



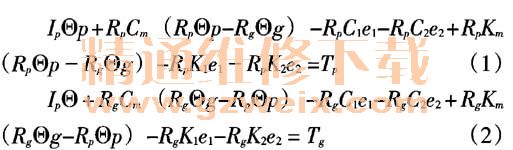
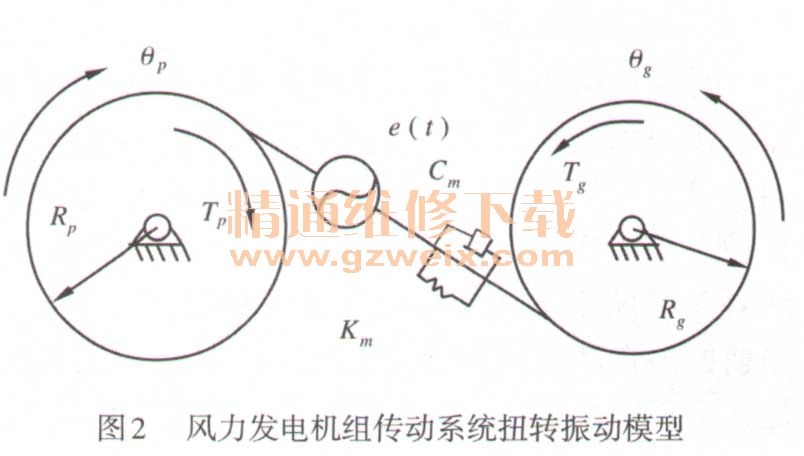
    在上述方程组的两个表达公式中，其中的Op主要代表的是主动出轮的扭转振动基本位移情况及其效率，而Og则表示的是被动出轮情况下的扭转振动位移。TP/T9分别代表的是作用在主动与被动车轮上的外载荷力矩。Ep、eg代表的是齿轮副间的误差。Cm代表的是齿轮副的啮合阻尼。凡与Rg分别代表的是主动与被动齿轮的基圆半径。IP /Ij分别代表的是主动与被动出轮的转动惯量。

[1] [2]  下一页