连续解析法的另一个分支是渐近法。其前提是待解方程存在小参量。 一般的，开关变换器的状态方程可写为：

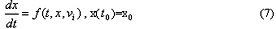
x是状态变量，v 为输入。对于理想开关，f有跳跃，但在Caratheoreodory意义下满足

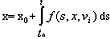
的x仍称为(４)的解[21]。因此，对（7）的求解有可能用渐进法。渐近法有KBM法、Ｖolterra 级数法[22]、多尺度法等。ＫＢＭ法对于分析瞬态过程及纹波颇有成效，常用于分析二阶系统，但是对于高阶系统求解太繁琐，且没将稳态与瞬态分开。另外，对于谐振式变换器的状态方程，无法引入小参量，故不能用KBM法。Ｖolterra 级数法只适于分析弱非线性系统。多尺度法的缺点与ＫＢＭ法相同。另外有一种与渐进法颇为相似的是谐波平衡法，严格上讲，它不是渐进法，因为它不需小参数的存在，但它能估计高次谐波。最后，需特别指出的是丘水生提出的等效小参量法[22，23]，它是近年来发展起来的精度高且分析简单的适于求解强非线性高阶系统的一种符号分析法, 是渐进法的一种[24]。其实质是在谐波平衡法中引入扰动技术，把周期解表达为按等效小参量展开的三角级数，避免求解变量较多的非线性代数方程，因此计算量大大减少，且可以获得闭环系统稳态直流解，占空比、输出纹波的解析解，并能直接说明纹波对占空比的影响及其同开关频率的关系，为设计提供依据。此法已被应用于PWM变换器和准谐振变换器的稳态分析[25，26], 在开关频率较低、纹波较大时仍获得很高的精度。另外此法还被发展, 提出了适合瞬态分析的等效小参量法[27]。目前此法得到了广泛的应用和推广。

4 结 语

本文对PWM开关变换器的分析方法作了一个较为全面的回顾与总结，对各种方法做了说明和评价。综上可知，离散法的发展缓慢，连续解析法的发展已有一定成效，但有些方法还需提高精度。

上一页  [1] [2] [3] [4] [5]