5.D4=B+D+E
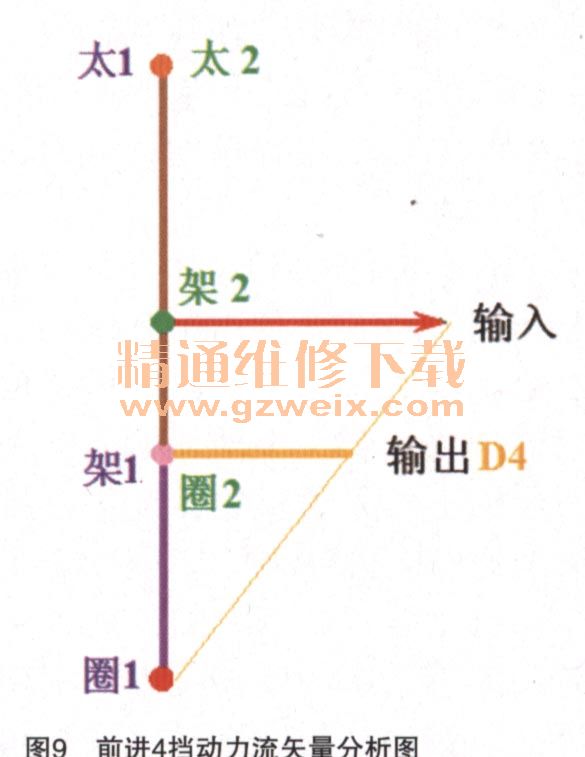
    当变速器进入4挡，离合器C松开，离合器D开始接合，输入轴不再由离合器C输入给第三排齿圈3以及第四排太阳轮4，而是仅由第二排行星架2常输入；由于第二排行星齿轮机构中，并没有相对固定的部件，那么行星架2的动力将按照以后的关系按照比例送给第二排太阳轮2以及齿圈2；那么由于离合器E接合，那么第三排太阳轮3就等于直接连接到了齿圈3，所以此时第三行星排就是传动比为1的状态，3个部件整体旋转；而又由于离合器D接合，那么第四行星排的行星架4又等于第三行星排的行星架3等于齿圈3，也就等于了第四排的太阳轮4；同理，在第四排中又有两个部件直接相连，所以此时第四行星齿轮机构也是传动比等于1的状态整体旋转；反向来推导，也就是说作为输出的行星架4等于行星架3等于第二排齿圈2，也等于第四排齿圈4等于第一排的行星架1．

    所以此挡位时，动力的变速过程仅发生在第一、第二两排行星齿轮机构上，而输入为第二行星架、公用太阳轮、固定为第一齿圈、输出为第一行星架1与第二齿圈2；回到我们最开始的话题，第二行星齿轮机构的输出，完全是由第一行星组的行星架1与太阳轮1的齿数关系来决定的第二排齿圈2与太阳轮2的输出比例关系。

    我们把上面这些连接关系简化成一张简单的动力传递图，如图8所示。

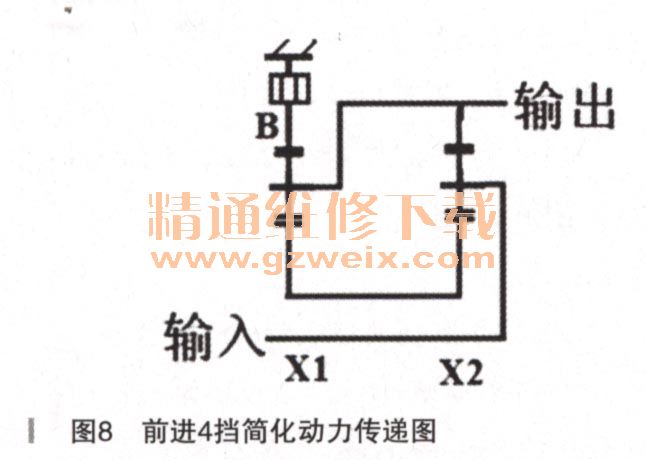
    实际上，在前进4挡，由于第三、第四行星排由于离合器D、E的连接关系而处于传动比等于1的状态而整体旋转，但是它们却实实在在的参与了动力流的传递过程；因此说，前进4挡是由全部四排行星机构作用的结果，只不过第三、第四行星排是等速传动的状态，第二排是由第一排决定的比例的减速输出。
    根据单排单级行星齿轮传动公式，以及各个部件的固定与连接关系我们得出下面的方程式组与条件：
    n太1+aln圈1＝（1+a1）n架1；
    n太2+a2n圈2＝（1+a2）n架2；
    n太1=n太2，n圈1=0；
    n架2＝输入，n圈2=n架1＝输出；
    此时我们由上面算出的第2排a2：a1=2，a2=2；
    在此我们不在反向推导某行星排的传动系数，由此可以直接计算出4挡传动比：
    i4=输入／输出＝n架2/n圈2=5/3=1.6666666。

    因此，通过这一次直接计算出来的传动比与资料中的i4=1 .67相等，恰恰就可以证明我们以前所反向计算出来的a1与a2是完全正确的！

    根据上面的动力流分析，笔者绘制了前进4挡的动力流矢量图，如图9所示。

      6.D5=B+C+D
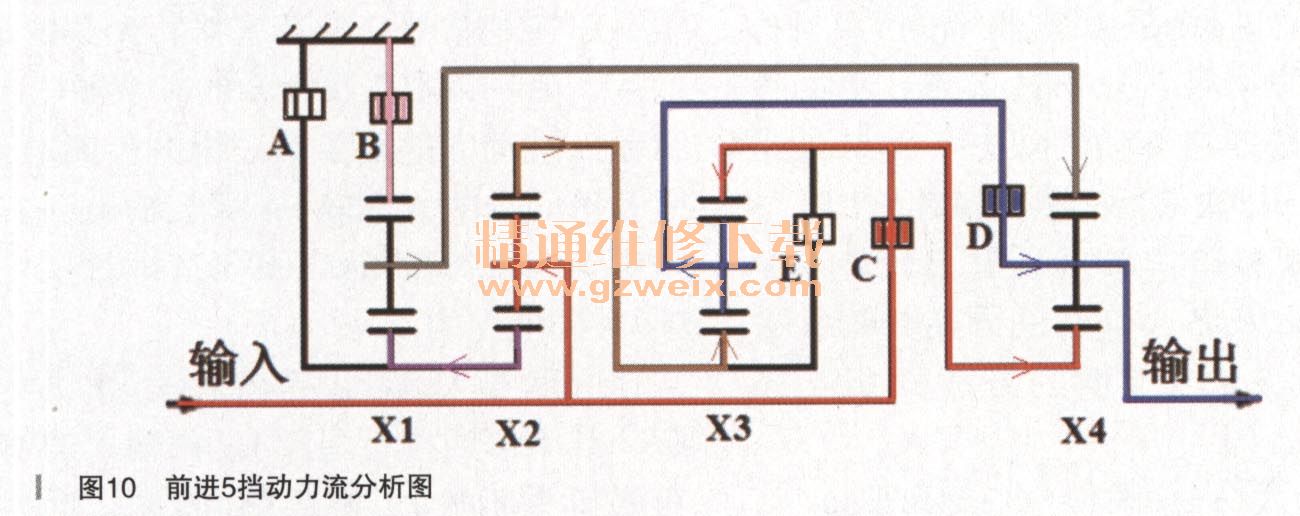
    当变速器进入5挡，离合器E再次松开，而离合器C再次接合，输入轴动力再次经两路流向行星组中，其中一路还是常啮合的第二排行星架2输入，另一路则再次接合的离合器C将输入轴动力送给了第三排的齿圈3以及第四排的太阳轮4，那么输出则是由第四排行星架4以及第三排行星架3共同输出的。

    这两部分输出笔者将分开讲解，其中第四排行星架4是由输入的第四排太阳轮4以及齿圈4驱动，而第四排齿圈4又是由第一排太阳轮1驱动行星架1获得的；此时第一排的齿圈1是由离合器B固定的，而作为输入的第一太阳轮1则是由第二排行星架2驱动太阳轮2和齿圈2获得的太阳轮2那一部分动力；而第三排行星架3作为动力输出的部分动力是由离合器C接合后把输入动力给第三齿圈3，第三太阳轮3的动力则是由第二排行星架2驱动太阳轮2和齿圈2获得的齿圈2那一部分动力作为输入的，所以才得出第三行星架3的输出。

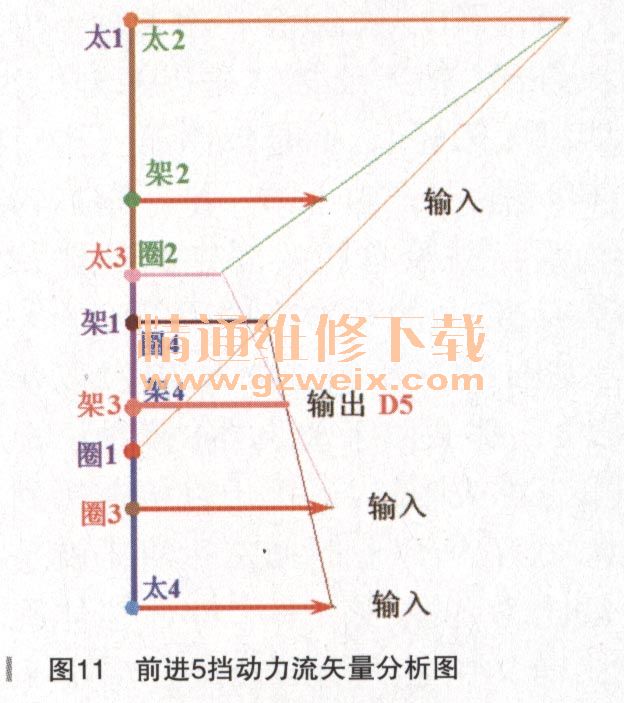
    以上我们可以看出，至此为止，ZF的8HP变速器的前进5挡是由四排行星齿轮机构共同作用的结果，每个行星齿轮机构都在以不同的转速旋转，而没有任何一个有传动比为1的整体旋转，所以我们说，这个挡位的动力流才是该变速器的难点中的难点，需要我们花大力气研究和理解。

    实际上在前进5挡，由于行星架2和离合器C的接合使得输入轴动力分别给了第二、第三、第四排，但是它们却均处于一个部件输入、两个部件输出的无效状态；而第一排的齿圈1被离合器B固定，就约定了第一排行星架1与太阳轮1的转速关系；又因为诸多的连接关系，就使得第二、第三、第四排行星齿轮机构有了错综复杂的约束关系，从而形成了一个极其复杂的输入、输出关系。笔者就该挡位的动力传动制作一张动力流向图，如图10所示。

    根据单排单级行星齿轮传动公式，以及各个部件的固定与连接关系，我们得出下面的方程式组与条件：
    n太1+a1n圈1= （1+a1）n架1；
    n太2+a2n圈2= （1+a2）n架2；
    n太3+a3n圈3= （1+a3）n架3；
    n太4+a4n圈4= （1+a4）n架4；
    n圈1=0，n太1=n太2， n架1=n圈4，n圈2=n太3；
n架2=n圈3=n太4=输入，n架3=n架4=输出。
    我们假设已知各个行星排的传动系数分别为：
      a1=1 ．98844，a2=2，a3=1．625（由下面第7挡推算出）a4=3.70；
    那么我们可以就去推算前进5挡的传动比i5。
    由上公式及条件，得出：
    太1+0=3架1；
    太2+1.988圈2=2.988输入；
    太3+1.625输入＝2.625输出；
    输入＋3.7圈4=4.7输出；
    又因为：n太1=n太2，n架1=n圈4，n圈2=n太3；
    所以：
    3圈4+1.988太3=2.988输入；
    太3＋1.625输入＝2.625输出→太3=2.625输出-1.625输入；
    输入＋3.7圈4=4.7输出→圈4=
  （4.7输出-输入）/3.7；
    所以：
    3（4.7输出-输入）/3.7+1.988
  （2.625输出-1.625输入）=2.988输入；
    所以：
    3.8108输出-0.81081输入+5.2185输出-3.2305输入=2.988输入；
    所以：
    9.03输出=7.03输入；
    所以：
    1  5=输入／输出=9.03/7.03=1.2845。
在此由上的计算结果，我们得出一个极其复杂的方程式组，经过一系列的约减，得出最终转动比与资料中（i5=1.29）完全是相对应的；同时这也说明，通过该挡位计算出来的传动比，恰恰就可以证明我们以前所反推算出来的a1 a2、a3、a4是正确的（a3是由以后的第7挡反向推算出来的）！

    根据上面的前进5挡的动力流传动分析，笔者绘制了前进5挡的动力流矢量图，如图11所示。

      7.D6=C+D+E
    当我们分析完ZF 8HP中最为复杂的前进5挡后，变速器终于迎来最简单的挡位：前进6挡。当变速器进入前进6挡后，离合器B终于完成了前进1～5挡中固定第一排齿圈1的作用，而离合器E反复无常的再次被接合，输入轴动力虽然还是通过两路输送给第二排行星架2与离合器C，但是由于离合器B的松开就使得第一排行星齿轮机构对第二排没有任何约束了，所以动力流则是从离合器C流入第三、第四两个行星机构的。

    那么由于离合器E接合，又使得第三排的齿圈3与太阳轮3直接连接，造成了第三排行星齿轮机构传动比为1整体旋转；而离合器D的接合，仍然使得最为输出的第四排行星架4与第三排行星架3相连，所以作为输出的行星架3是与输入轴齿圈3是传动比为1同向相等的转速关系。

    实际上前进6挡时，由于行星架4等于输入等于太阳轮4，所以第四排行星机构也是传动比等于1的工作状态；由于第二齿圈2也等于输入轴，所以第二排行星机构也是传动比等于1的工作状态；而由于第一排的行星架1等于输入等于太阳轮1，所以第二排行星机构也是传动比等于1的工作状态；因此在前进6挡时，所有行星齿轮机构的转动状态都是最简单的转动比为1的工作状态。
    但是虽然第一、第二、第四排的行星机构都在等速与输入轴旋转，但是由于离合器A、B没有对它们有任何约束关系，所以我们说：第一、第二、第四排的行星机构并不真正的参与动力传输，仅仅第三排行星机构在传递动力流。

[1] [2]  下一页