与发达国家相比，中国汽车工业相对落后，自动变速器技术方面更是相差一大截。面对这样的状况，进一步精确分析变速器行星齿轮机构的传动比、控制规律及动作顺序就显得越来越有意义。
    一、杠杆法简介
    二十世纪70年代末和80年代初，美国通用公司开始采用杠杆模拟法（简称杠杆法）分析行星齿轮系的传动特性。
      1．定义
    行星齿轮的杠杆分析法是将行星齿轮减速机构转换为等效垂直布置杠杆系统，然后通过分析垂直布置的杠杆，间接分析行星机构的方法。
      2．原理
    （1）行星排等效杠杆图
    垂直杆把1个行星排上的元件简化为3个点，3点分别代表太阳轮S、行星架PC和齿圈R，如图1所示。

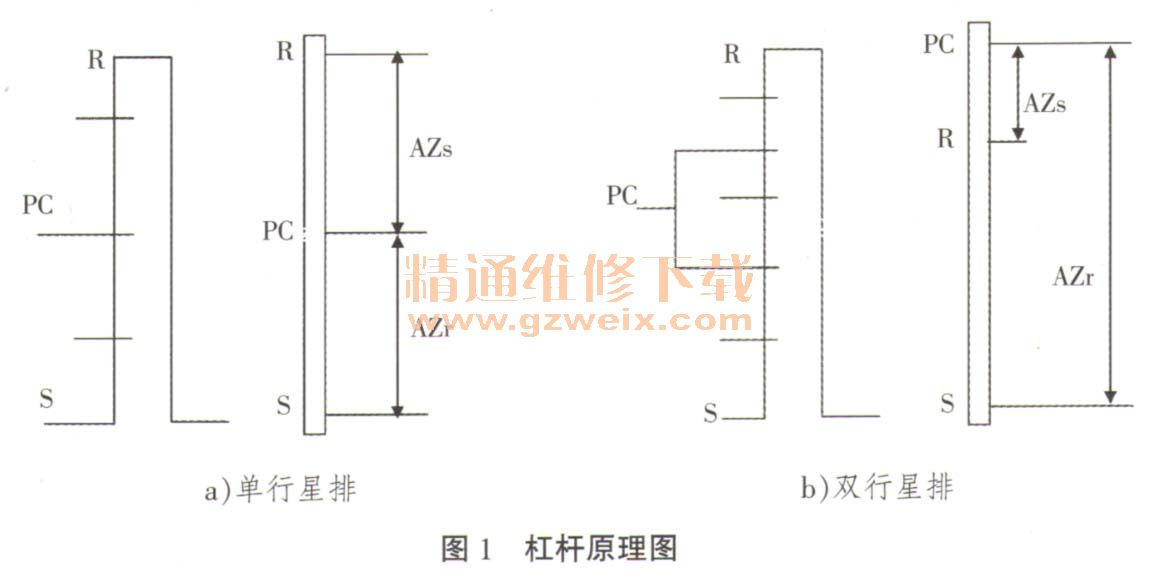
    单行星排：中心支点为PC，两头支点分别为S和R（如图1a）所示）。
      双行星排：中心支点为R，两头支点分别为PC和S（如图1b）所示）。
    点S和点R离中间点PC的长度分别和齿圈与太阳轮的齿数成正比，图1中A为任意比例常数；以1个垂直杠杆替换1个行星排，行星排3元素的速度转化为支点的水平角速度，其水平角速度符合行星排的转速方程式。
      （2）行星机构等效杠杆图
    行星轮系是由多个行星排组成，因此将杠杆分开画，行星排与行星排连接点用1水平线连接，并调整两端支点到中间支点的长度，可是连接点到中间支点的长度是一样的，而且行星排长度比与齿数比保持不变。如图2所示。

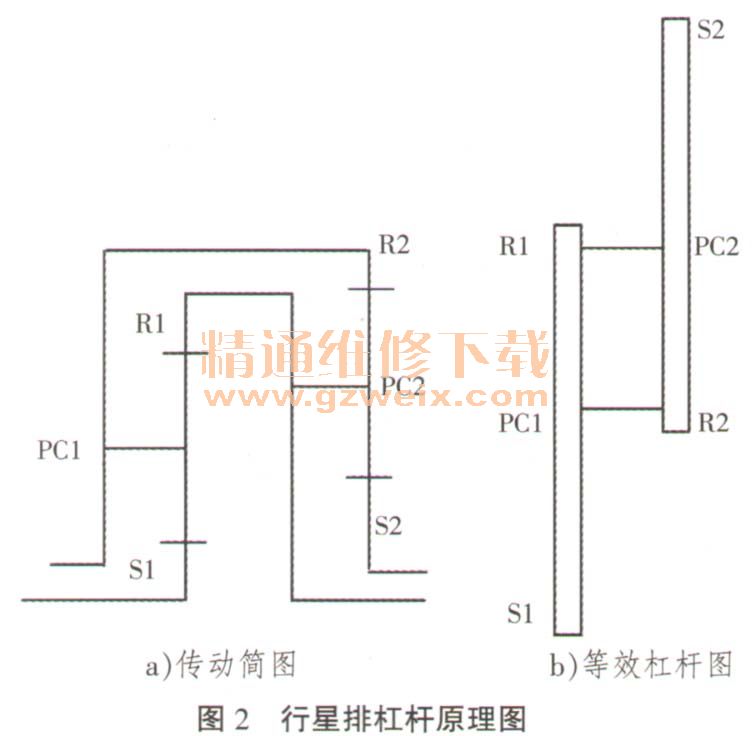
    利用三角形相似原理就可以得出杠杆法的水平角速度符合转速方程式。
    二、杠杆法分析实现6挡变速器的可能性
    目前市场上销售或在用的轿车部分配备的是4挡自动变速器，采用的是双排行星齿轮机构，其无法实现5个、6个或者更多的前进挡位，所以如果要实现更多的前进挡位，必须再加入1组行星排，目前可采用2种形式：
    串联式：在原有的双行星排变速器输入轴、输出轴与行星齿轮系增加，但换挡控制将更复杂。
    并联式：三排行星机构依次组成的并行传输，结构紧凑。
    3个行星排机构等效杠杆输出点的可能性分析与双排行星齿轮类似的分析，3个行星排等效杠杆图并联为杠杆图，因为有3个要素是重叠在一起成1个点，所以杠杆图将只有5分，分别作为输入、输出、制动和中间接触。从端点的输出，有3种可能。

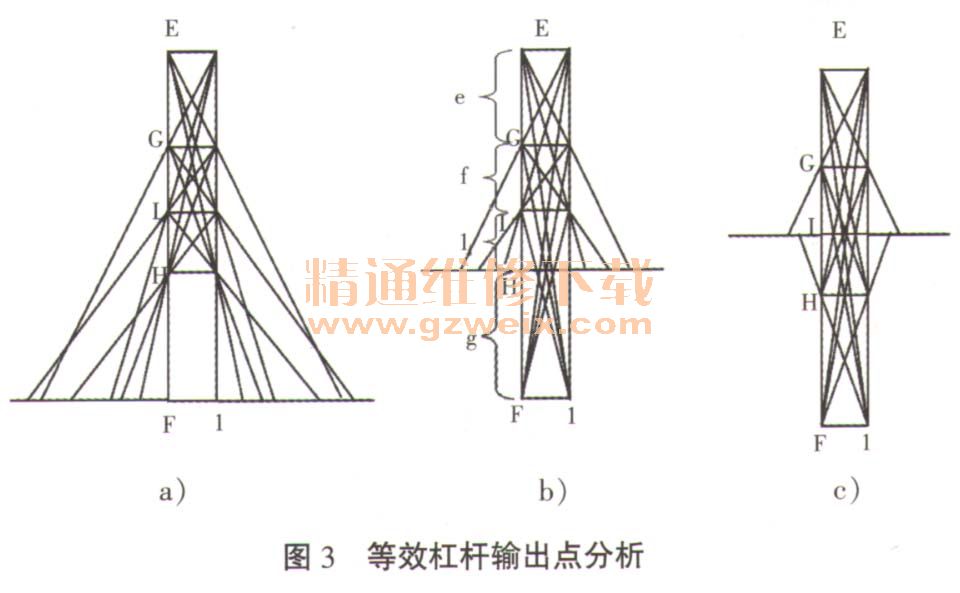
      （1）以端点F（E、F端点是等价点）为输出点，如图3a）所示。
    通过排列组合的方法改变输入点和制动点，分析杠杆可以得到6个反向车速（角速度比小于0的）、6个超速挡（角速度比小于1）、1个直接挡（角速度比等于1），没有减速齿轮（角速度比大于1）。因此不满足传动比的要求。
    （2）以中间点H（G、H两中间点是等价点）为输出点，如图3b）所示。
    通过排列组合的方法改变输入点和制动点，分析杠杆可以得到反向车速（角速度比小于0）、3个超速挡（角速度比小于1）、1个直接挡（角速度比等于1）、6个减速挡（角速度比大于1），因此满足要求。
      （3）以中央点I为输出点，如图3c）所示。
    通过排列组合的方法改变输入点和制动点，通过分析杠杆可得2个反向车转速（角速度比小于0）、2个超速挡（角速度比小于1）、1个直接挡（角速度比等于1）、6个减速挡（角速度比大于1）9因此满足传输要求。
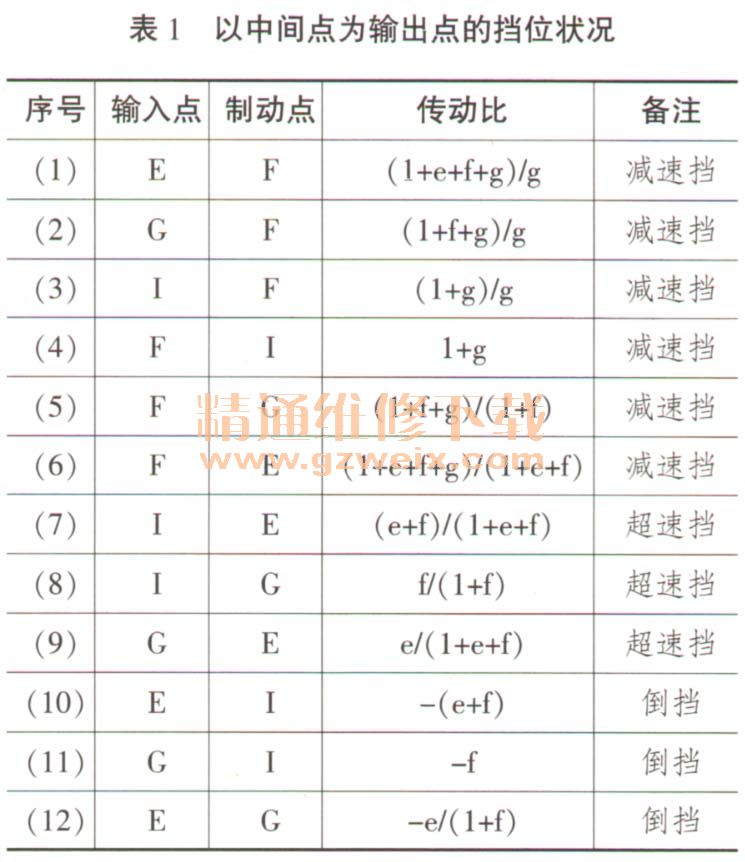
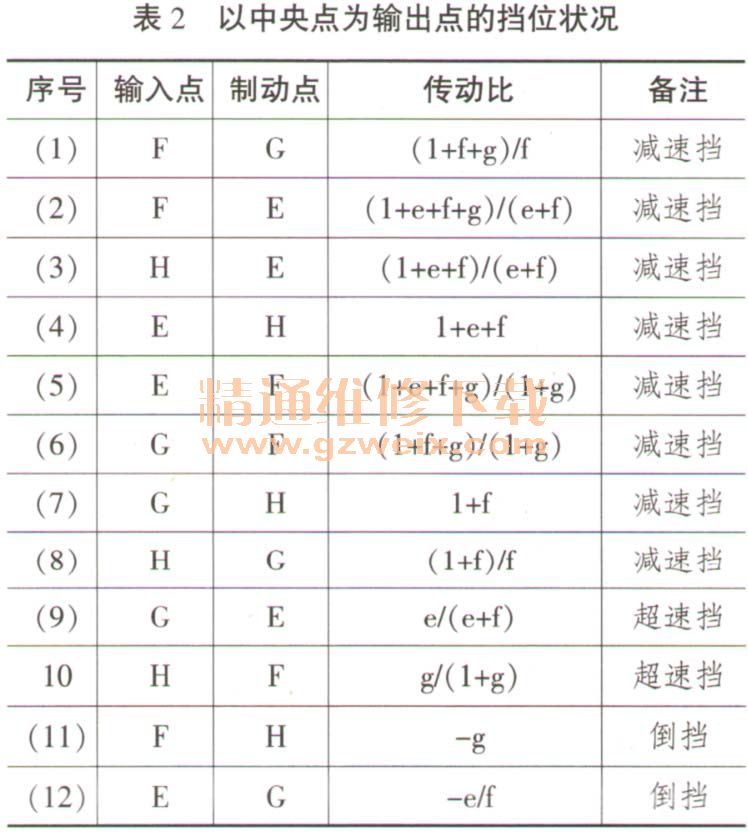
    综上所述，并联式三排行星轮可以提供表1和表2中所列的挡位。

[1] [2] [3]  下一页