当前随着网络的普及，通信便捷和信息安全之间的矛盾就越来越突出了，如何保护信息不被非法获取、篡改和盗用已成为研究的热点。信息安全技术经过多年的发展，对信息的保护已从密码技术发展到了隐藏技术，但在信息隐藏技术的应用过程中，如果单纯地用各种信息隐藏算法对秘密信息进行隐藏保密，那么攻击者只要直接利用现有的各种信息提取算法对被截获信息进行枚举运算的话，就很有可能提取出秘密信息。但如果在信息隐藏之前，先对秘密信息按照一定的运算规则进行置乱处理，使其失去本身原有的面目，然后再将其隐藏到载体信息里面，即使攻击者将秘密信息从载体中提取出来，也无法分辨出经过置乱后的秘密信息到底隐藏着什么内容，所以对秘密信息进行置乱运算是很有必要的。关于图像置乱的研究已有很长时间，以 Hilbert曲线、Arnold 变换和幻方置乱为代表的算法主要存在两点不足: ( 1) 要进行多次重复置乱，才能达到满意的置乱效果; ( 2) 置乱变换的参数少，从而使得用于图像加密时的密钥量小。如果攻击者不在乎时间长短，对秘密图像进行枚举运算，还是有可能将秘密图像还原的。为了提高图像的置乱效果和增加图像置乱加密的密钥量，通信双方可事先约定一个密钥文件，文件中多个单独的密钥，这些密钥记录各种置乱算法运算的先后顺序以及各自的置乱次数，接收方根据事先已有的密钥文件就可以很轻松地还原出原始图像，方便快捷。同时，由于密钥量的增加，又提高了传输信息的安全性。

1 密钥的生成

通信双方事先约定一幅灰度图像( 如果是彩色图像，则选择其红、绿、蓝 3 个颜色通道中的一个) ，该图像双方都有或能够同时获取的、与将要传输的图像大小完全相同的数字图像，记为 f( x，y) ，大小为m × n，作为密钥的模板，进行如下操作:

( 1) 找到并将图像 f( x，y) 中灰度值最小的像素赋值为 0; 剔除该像素后，再找到剩余像素中灰度值最小的像素，再将其赋值为 1，然后剔除; 依此类推，最后将图像 f( x，y) 中灰度值最大的像素赋值为 m ×n。同样，也可以反过来，将图像 f( x，y) 中灰度值最大的像素赋值为 0，将灰度值最小的像素赋值为 m ×n，从而形成另一种密钥。

( 2) 对于图像 f( x，y) 中灰度值相同的像素，一幅灰度图像总有相当数量的像素灰度值相同，可以按照像素的位置关系确定赋值顺序。位置关系的查找方法也是密钥的组成部分。例如从上到下、从左到右; 从下到上、从右到左等; 还可以采用如图 1 所示的 Z 形查找方法。

 ( 3) 经过前两步的操作，得到的图像记为 f1( x，y) ，其大小为 m × n，全部像素值从 0 到 m × n 均匀分布，每个像素有且仅有惟一的正整数值。将图像f1( x，y) 的全部偶数行提出，构成图像 1; 再提出全部奇数行构成图像 2，连接图像 1 和图像 2，构成与原图像同样尺寸的新图像; 对新图像的列进行同样的操作。例如 1、2、3、4、5、6、7、8 代表图像行号，重排 1次变为: 2、4、6、8、1、3、5、7，重排 2 次变为 4、8、3、7、2、6、1、5。如图 2 所示。

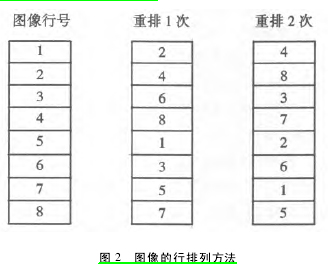
注意: 并非重排的次数越多越好，上例的 8 行重排 6 次就还原了。重复 H 次，得到图像 f2( x，y) ，H为密钥的一部分。

综上所述，生成的密钥包括: 赋值方式、赋值顺序、重排的次数和图像 f( x，y) 。

2 置乱操作

通信的信源方，所要传输的灰度图像( 如果是彩色图像则表示某一个颜色通道) 记为 H( x，y) ，进行如下操作:

( 1) 将灰度图像 H( x，y) 变成单列矩阵 A，使每一个图像像素都有一个惟一的地址( 单列矩阵的行号) 。

( 2) 再将图像 f2( x，y) 变换成单列矩阵 B。

( 3) 建立一个与 A、B 等长的单列矩阵 C，C 中存放以矩阵 B 的元素值为地址的矩阵 A 的元素。例如A( 1) = 162、A( 2) = 79、A( 3) = 196，B( 1) = 2、B( 2)= 3、B( 3) = 1，则 C ( 1) = 79、C ( 2) = 196、C ( 3) =162，排列规律为 C( i) = A( B( i) ) ，i 为行号。如图 3所示。

[1] [2]  下一页