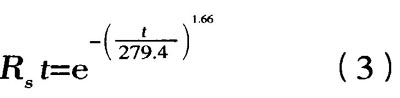由图4可知，轮毂轴承中的滚动体的可靠度比较高，因为轮毂轴承在制造时对滚动体做了相关的热处理，增强了其使用性能。轮毂轴承的内圈是可靠度较差的一个元件，轴承内圈受力较大，这与轮毂轴承有限元分析的结果相同，可以以此为依据，在制造过程中考虑对轴承内圈进行特殊处理，以延长轴承的使用寿命。
    由串联系统可靠度的计算方法，将数据（t、 Ri（ t））（i=1、2、3、4）进行最小二乘拟合。最小二乘拟合是一种数学上的近似和优化，利用已知的数据得出一条直线或者曲线，使之在坐标系上与已知数据之间的距离的平方和最小。通过最小二乘拟合，可以得到轴承寿命的分布估计值为ms=1.66，ηs=279.4，由此得到轴承的可靠度函数为

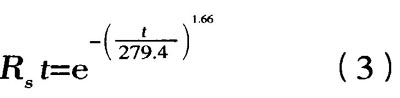
    对应的可靠度曲线如图5所示。

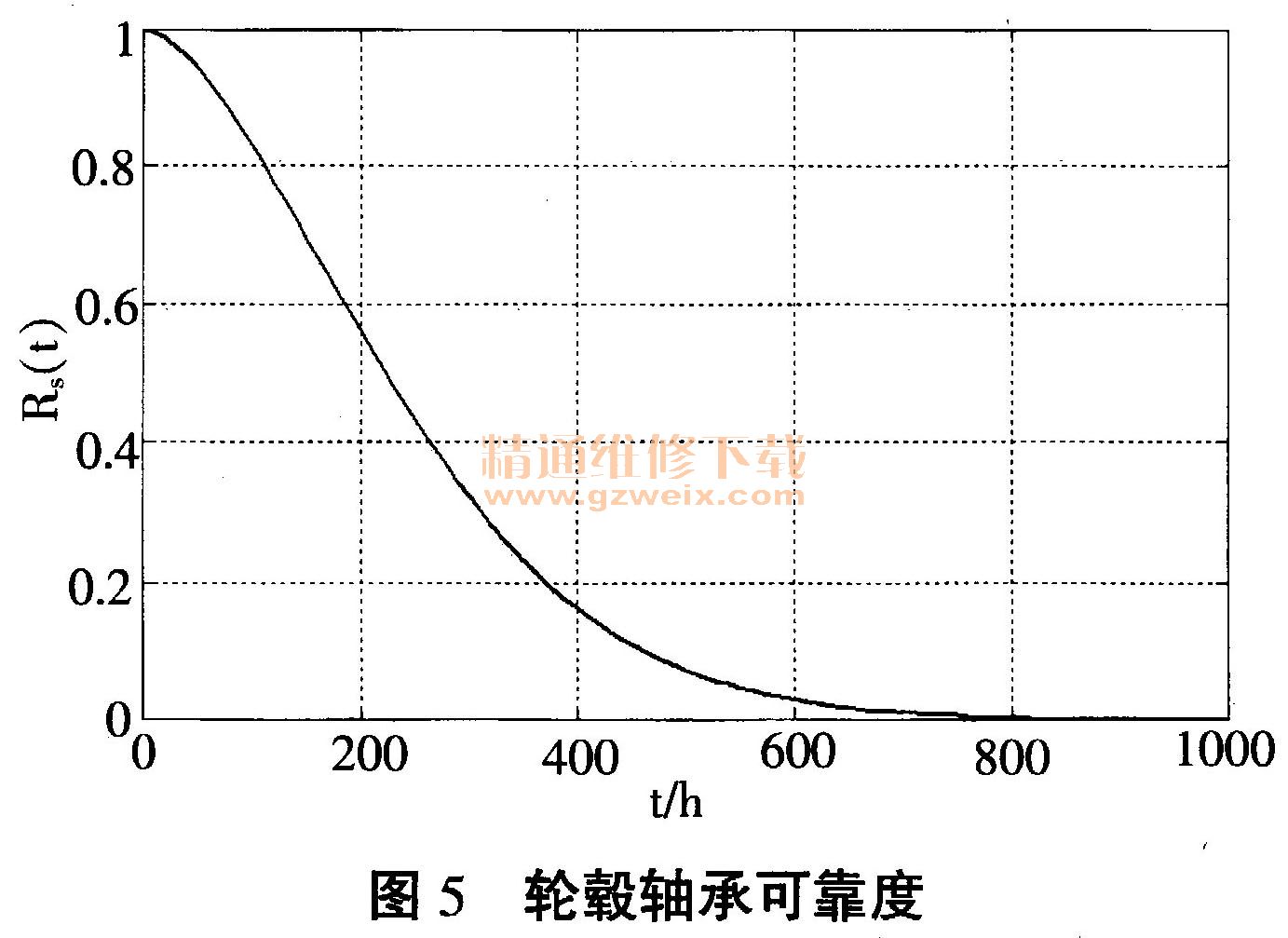
    由图5可知，轮毂轴承在100～300h的时间段内，可靠度迅速减小，当轴承运行之后，可靠度变得较小。此外，由试验结果可知，轮毂轴承系统中，内圈是最容易损坏的，是影响系统可靠性的主要因素，若想提高系统的可靠度，须优先从内圈考虑，如使用强度和耐磨性更高的结构钢，采用更先进的淬火工艺。从寿命计算中可知，零件的表面粗糙度也会严重影响其使用寿命，因此对轴承内圈采用更先进的抛光工艺也是提高其可靠性的有效手段。

    四、小结
    使用威布尔分布作为轴承的可靠性分布函数，并以此确定可靠度的表达式，之后使用贝叶斯理论，选用贝塔分布作为先验分布，进行威布尔参数估计。以某厂家的轮毂轴承为样件，进行可靠性试验，确定试验方法和抽样方案，之后使用试验数据进行威布尔参数估计，得到各元件和系统的可靠度曲线。

上一页  [1] [2]