说明 ：在上面的动力矢量图中，其太阳轮、行星架、内齿圈在竖轴上的位置关系是确定好的，在单排单级行星齿轮机构中，行星架必须处在另外两者的中间 ；而单排双级行星齿轮机构上，内齿圈必须处于两个部件的中间 ；这个规定是由行星齿轮机构的结构所决定的，在此不做论述。

在单级行星齿轮机构中，行星架在数轴上对应的位置与齿圈和太阳轮的齿数比是相互关联的；假设N太=30齿，      N圈=         90齿，    那么，L（架-太）之间的长度就是L（圈-架）之间的长度的三倍，即：N太/N圈=L圈-架/L架-太。而横轴则是代表了该部件的转速，同样以上面假设的齿数关系，当行星架固定不动、太阳轮输入、齿圈输出的情况时,此时传动比a=输出轴转速／输入轴转速=内齿圈齿数/太阳轮齿数=N圈/N太=          L架-太/L圈-架=90/30=3         。

同样，在图 4 中的单排双级行星齿轮机构中，由于行星架上的行星齿轮为两排，所以其内齿圈位置与行星架互换了传递关系，但其内齿圈的比例关系同样适用，在此不再复述。

需要我们注意的是以前常见的行星齿轮结构驱动矢量分析，而如今在一些高挡位的自动变速器上，如 6 速、7 速、8 速等自动变速器中还会有另外一些特殊的驱动模式，就是行星齿轮结构的 3 个部件不再是简单的固定、输入、输出关系互换，而可以是以 2 个不同数值的输入量来决定一个输出量或者仅有一个输入量来获得两个输出 ；其实这些特定的驱动模式无外乎就是行星齿轮结构中的 3 个部件：（1）如果知道两个部件的输入量，那么就可以获得第 3 个部件的输出 ；（2）如果只知道 1 个部件的输入，却知道另外 2 个部件的输出比例关系，所以仍然可以按照约束关系算得 2 个输出；但是如果仅有 1 个部件输入，没有其他任何约束条件，当然也就无法获知输出了 ；这些都是可以通过方程式验证和证明的，在此不做详述。这些特殊的驱动模式矢量坐标图如图 5 所示。有了对上述两种行星齿轮结构的驱动模式的简单了解后，下面我们再就上述驱动模式的传动比计算简要的进行说明。

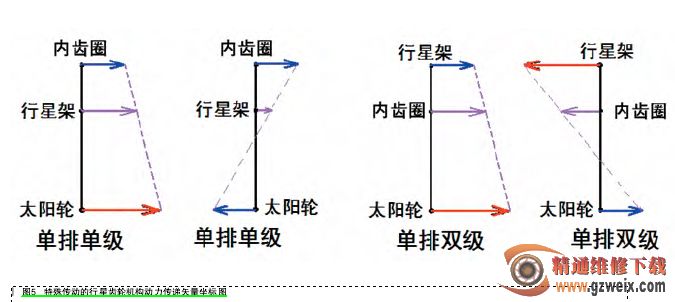
1. 单排单级行星齿轮机构说明

常见的单排单级行星齿轮机构的齿数的关系一般情况为 ：行星架齿数＞内齿圈齿数＞太阳轮齿数 ；备注 ：本来行星架是没有实际齿数的，但是为了方便行星齿轮机构的计算与说明，我们可以特意给行星架规定一个虚拟的齿数 ；如果 N太为太阳轮齿数=30，       N圈为内齿圈的齿数 =90，那么N架为行星架的虚拟齿数就等于 N太+      N圈的齿数 =120。

则单排单级行星齿轮机构传动比的计算公式为 ：n太+an圈-(1+a)n架=0。

说明 ：n太= 太阳轮转速 ；n圈=内齿圈转速 ；n架= 行星架转速 ；a=内齿圈齿数 / 太阳轮齿数 ；

该传动机构按照不同的固定、输入、输出部件，有如下几种动力传动效果（如表 1 所示）。

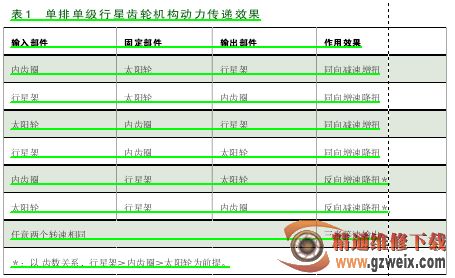
2. 单排双级行星齿轮机构说明

常见的单排双级行星齿轮机构的齿数的关系一般情况为 ：内齿圈齿数＞行星架齿数＞太阳轮齿数 ；备注 ：同样在双级行星齿轮机构中行星架也是没有实际齿数的，但是为了方便行星齿轮机构的计算与说明，我们仍可以给行星架规定一个虚拟的齿数 ；如果 N太为太阳轮的齿数 =30，     N圈为内齿圈的齿数 =90，那么 N架为行星架的虚拟齿数就等于 N圈减去 N太的齿数，即 N圈—N太=60。

那么，单排双级行星齿轮机构传动比的计算公式为 ：n太-a         n圈+(a-1)n架=0

说明 ：n太= 太阳轮转速 ；n圈=内齿圈转速 ；n架= 行星架转速 ；a=内齿圈齿数 / 太阳轮齿数 ；

这种传动机构按照不同的固定、输入、输出部件，有如下几种动力传动效果，如表 2 所示。（待续）

上一页  [1] [2]