2.1第1个核心----高效的数学分析模型
    1）模型公式及变量介绍

    式中：χi（i=1～50＋）----线束单价；yi（i=1～200＋）----细分车型销量；9----线束零件号数量；k----单位零件号物流投入系数；：----总车型数量；ai（i=1～40＋）----每个配置成本；ti（i=1～40＋）----每个线束含配置数；Xj----线束配置组合；Yi----车型配置组合；G----总成本投入；a----线束相关配置；t----线束相关配置数量。求解拜口a使得C有最小值。
    2）模型公式说明
    单个线束零件的单价成本＝该线束总成包含的每个配置成本之和；单个线束零件的累计成本＝该零件的单价成本x采用本零件涵盖车型的销量小计；总的线束零件的总累计成本＝每个线束零件的累计成本之和；总的物流成本＝线束零件状态数量x单个零件平均所需的物流成本投入系数。上述各项成本累加便是本项目总的成本投入。形成数学分析公式后，求解线束配置组合数量（t）和每个线束所带的具体配置组合（a），使得总成本投入有最小值。
    2.2第2个核心—高效的实现算法（目标拣选算法）
    有了数学分析模型还不够，高效的算法实现才能提升分析效率。最常规的实现算法是“穷举法”，其计算过程是：先利用计算机快速的运算速度，不断将各种线束配置的搭配组合代入上述数学分析模型进行分析计算，然后循环选取总成本最低的一系列组合就是最终结果。但是根据线束的关联性（常规的车型线束一般与整车40多个配置相关），完全把排列组合打散开将会存在数百亿种排列组合，数量相当庞大，如图4所示。

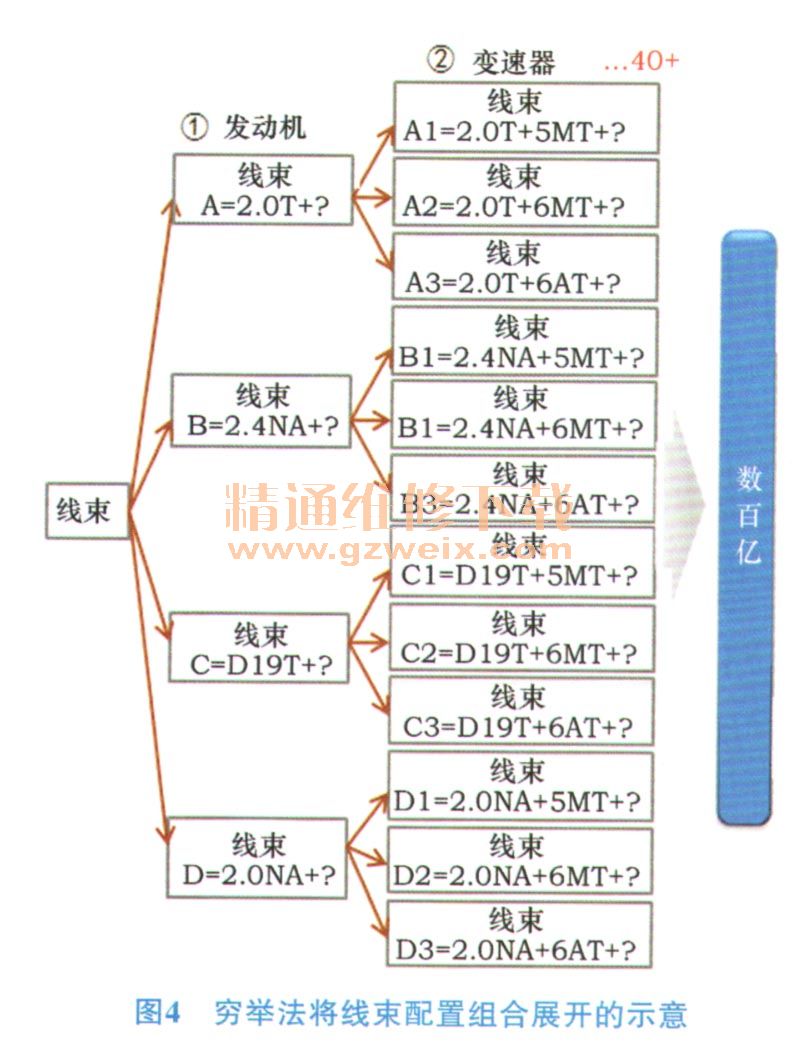
    如果采用穷举法，经过实测，由于排列组合的数据量过大，普通工作站需要花数小时甚至数十小时才能完全分析处理完。因此，选取一个更先进的算法来实现分析过程尤为重要。最终，经过实测，目标拣选算法成为最优算法。此算法过程如图5所示。

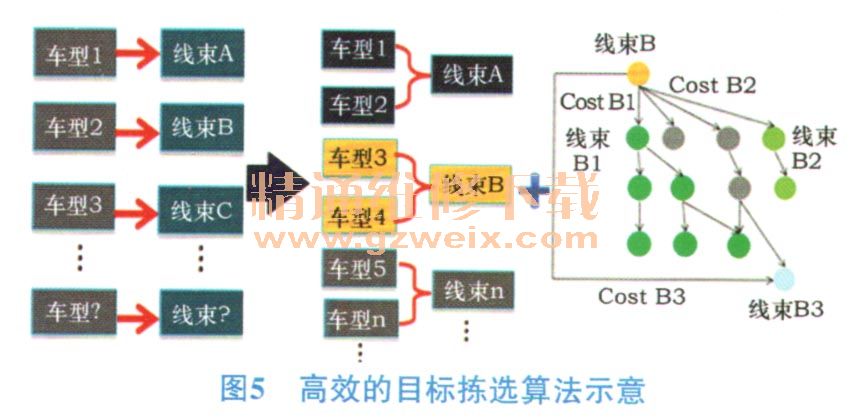
    算法过程解释如下：先将车型组合分区（可实现线束配置高低配涵盖兼容的车型在同一个分区中），同一分区中拣选一个配置最高的线束作为目标，由于不同分区之间的线束不存在相互兼容涵盖的关系，因此仅需要计算本分区中各种高低配线束之间的成本对比。这样一来，加权循环的计算量大大减少，经过笔者实测，普通工作站仅需数十秒甚至数秒即可完成分析处理，大大提高了效率。

    3 本设计辅助工具的预估收益
    经过建立数学分析模型和高效的算法实现，一套线束配置智能化设计分析软件工具便顺利完成。通过利用这套工具可以对商用车的线束配置设计起到非常好的设计辅助作用，大大提高效率和准确率。同时，可以实现零件成本和物流成本的最大化节省，具体估算如下。
    1）零件成本方面线束配置可做到更精益化，减少线束功能预留（单辆车节省1～10元不等），按商用车车型常规5万辆／年左右的销量，预计一年可以节省50万元。
    2）物流成本方面经物流部门测算，每减少1个零件号，每年大约可节省10万元物流成本。运用此工具将最大程度减少线束数量，预计每年至少减少10个零件号，总计减少成本约100万元。
 

上一页  [1] [2]