式中RH ——霍尔系数（  ）；
IH——控制电流（A）；
B——磁感应强度（T）；
d——薄片厚度（m）；
p——材料电阻率（Ω*s）；
u——材料迁移率（ ）；
若在上式中各常数用KH表示，则有
E=KHIHB
　　霍尔元件产生的电动势很低，直接应用很不方便，实际应用时采用霍尔集成电路。霍尔元件输出电压的极性随磁场方向的变化而变化，直流无刷电动机的位置传感器选用开关型霍尔集成电路。
　　磁阻效应是指元件的电阻值随磁感应强度而变化，根据磁阻效应制成的传感器叫磁阻电阻。

 三相直流无刷电动机的运行特性
　　要十分精确地分析直流无刷电动机的运行特性，是很困难的。一般工程应用中均作如下假定：
（1）电动机的气隙磁感应强度沿气隙按正弦分布。
（2）绕组通电时，该电流所产生的磁通对气隙所产生的影响忽略不计。
（3）控制电路在开关状态下工作，功率晶体管压降 为恒值。
（4）各绕组对称，其对应的电路完全一致，相应的电气时间常数忽略不计。
（5）位置传感器等控制电路的功耗忽略不计。
　　由于假设转子磁钢所产生的磁感应强度在电动机气隙中是按正弦规律分布的，即B=BMsinθ 。这样，如果定子某一相绕组中通一持续的直流电流，所产生的转矩为
TM=ZDLBMrIsinθ
式中， ZD——每相绕组的有效导体数；
L——绕组中导线的有效长度，即磁钢长度；
r——电动机中气隙半径；
I——绕组相电流。
　　就是说某一相通以不变的直流后，它和转子磁场作用所产生的转矩也将随转子位置的不同而按正弦规律变化，如图5所示。

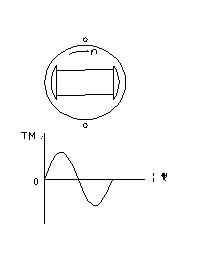
图5 在恒定电流下的单相转矩
　　它对外负载讲，所得的电动机的平均转矩为零。但在直流无刷电动机三相半控电路的工作情况下，每相绕组中通过1/3周期的矩形波电流。该电流和转子磁场作用所产生的转矩也只是正弦转矩曲线上相当于1/3周期的一段，且这一段曲线与绕组开始通电时的转子相对位置有关。显然在图6 a所示的瞬间导通晶体管，则可产生最大的平均转矩。因为在这种情况下，绕组通电120度的时间里，载流导体正好处在比较强的气隙磁场中。所以它所产生的转动脉动最小，平均值较大。习惯上把这一点选作晶体管开始导通的基准点，定为 。在 =0度的情况下，电动机三相绕组轮流通电时所产生的总转矩如图6b 所示。

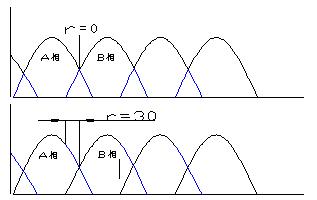
图6 三相直流无刷电动机半空桥转矩
　　如若晶体管的导通时间提前或滞后，则均将导致转矩的脉动值增加，平均值减小。当 =30度时，电动机的瞬时转矩过零点，这就是说，当转子转到某几个位置时，电动机产生的转矩为零，电动机起动时会产生死点。当 ≥30度后，电动机转矩的瞬时值将出现负值，则总输出转矩的平均值更小。因此，在三相半控的情况下，特别是在起动时， 不宜大于30度，而在直流无刷电动机正常运行时，总是尽力把 角调整到0度，使电动机产生的平均转矩最大。当 =0度时，可以求得输出转矩的平均值 ：

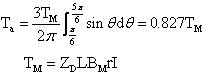
　　电动机在电动转矩的作用下转动后，旋转的转子磁场就要切割定子绕组，在各相绕组上感生出电动势，当其转速n不变时，该电动势波形也是正弦波，相位同转矩相位一致。在本电路中，每相绕组在一个周期中只通电 ，因此仅在这 期间对外加电压起作用。所以对外加电压而言，感生电动势波形如图7所示。

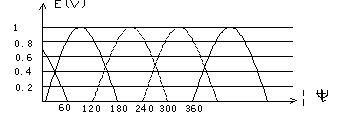
图7 三相直流无刷电动机半控电路的反电动势
　　同理可按下式求得感生电动势的平均值 ：

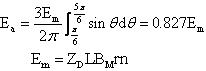
　　从上面的平均转矩和平均反电动势，便可求得直流无刷电动机稳定运行时的电压平衡方程式，为此首先定义反电动势系数和转矩系数：

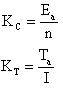
　　对于某个具体的电动机，它们为常数。当然，其大小同主回路的接法以及功率晶体管的换相方式有关。

上一页  [1] [2] [3] [4]  下一页