摘要：分析宏程序的构成规律，制定其设计方案，建立曲线段回转体宏程序加工模板，设置好参数于模板中，加工出相应精度要求的曲线段回转体工件。

    0 引言
    随着数控机床加工技术的快速发展，在数控车床加工中会经常遇到如椭圆、抛物线、双曲线等曲线轮廓回转体的加工，用常规的数控编程指令，需要计算每个节点的坐标值，不仅数学计算量大、加工精度差、编程复杂，而且容易出错、降低生产效率，若采用CAXA/MasterCAM软件自动编程，也需要大量时间来建模和数据处理，出现程序传输速度慢、空刀多、浪费时间、精度控制难等弊端。目前，数控车床的数控系统不仅向用户编程提供了一般的准备功能和辅助功能，而且有了扩展数控功能的宏程序加工手段，曲线轮廓零件的加工可以用宏程序，方便快捷。宏程序在数控车床加工中的运用很广泛，理解掌握它有一定的规律可以遵循，它有一定的编程模式，对于初学者，数控车床宏程序的学习要了解这个规律，尤其要精读几个有代表性的宏程序加工实例，在此基础上进行模仿，从而能够以此类推，达到独立编制宏程序的目的，收到较好的加工效果。
    所谓宏程序，将一组命令所构成的功能，像子程序一样事先存入存储器中，用一个命令代表，执行时只需写出这个代表命令，就可以执行其功能。这一组命令称为用户宏程序。用户宏程序按功能分有A和B两种类型，A类宏程序是以G65 Hx x P# x x Q# x x R# x x的格式输入的；而B类宏程序则以直接的公式和语言输入，和C语言很相似，在数控车床加工中应用广泛。我们先从B类宏程序的使用技巧入门。
宏程序属于高级语言编程范畴，它在程序主体中使用变量，对变量进行赋值，变量之间可以进行函数运算、逻辑判断和跳转等。尤其是同一类中的相似零件，只需运用宏程序指令对该组中某一零件进行编程，每次只改变其中变量的赋值，就可以加工这类零件中的其他零件。以下三个方面是B类宏程序的使用规律，仅供参考。

    1 数控车床宏程序的编程方案设计
    （1）确定自变量。通过工件轴线纵剖面的非圆函数曲线轮廓中的Z和X坐标都可以被确定为自变量，一般情况下会选择起点和终点坐标容易得出的而且便于编程的一个变量坐标作为自变量，还要考虑尽可能用一个函数表达式书写整段要加工的曲线轮廓，也就是尽量避免出现分段函数。
    （2）精确计算自变量始点和终点的坐标值（注意正负号）。必须明确要加工的轮廓是弧内侧或弧外侧，哪个部分；该坐标值是标准曲线自身的坐标系，而非工件坐标系；其始点坐标是曲线轮廓加工开始点的自变量坐标值，终点坐标为曲线轮廓加工结束点的自变量坐标值。
    （3）依据数学表达式，确定另一个变量相对于自变量的函数表达式（用数控系统宏程序的符号、格式编写）。
    （4）确定加工曲线自身坐标系的原点相对于工件坐标系原点的坐标偏移量（注意正负号）。
    （5）分析从始点到终点两个变量（自变量和函数）各自的变化规律，依据加工精度要求确定自变量的变化步距。
    （6）选择并确定循环语句格式。

    2 非圆曲线轮廓加工宏程序的编程模板
    在数控车床曲线轮廓加工中椭圆的例子较多，就以椭圆轮廓加工为代表分析宏程序加工编程过程。如图1所示，XOZ表示工件坐标系，即编程坐标系，X1 O1 Z1表示标准椭圆曲线坐标系。编写宏程序时还应注意以下几点：
    （1）工件的精度与编程时所选择的插补步进距离有关，步距值越小，加工精度越高，但会造成数控系统计算工作量加大，降低进给速度，即降低加工效率，在满足技术要求前提下，尽可能增大步距。
    （2）宏程序具有通用性，只需改变相应变量的赋值，如，椭圆两个半轴的赋值、坐标偏移距离赋值等，就可以加工同类零件。
    （3）可以采用IF...... GO TO或WHILE......Dom...... ENDm其中的任一中循环形式，但两种循环自变量、书写形式有较大差别，编写后效果相同。宏程序编制表如表1，坐标系关系图如图1。



    常数说明：
    a椭圆X方向半轴值；
    b椭圆z方向半轴值；
    Xa椭圆标准曲线坐标系原点0，到编程坐标系中心O的X向距离；
    Zb椭圆标准曲线坐标系原点0，到编程坐标系中心O的Z向距离；
    A点为椭圆曲线段加一工的起始点，该点的Z1坐标Az1为自变量的初始值；
    B点为椭圆曲线段加工的终止点，该点的Z1坐标Bz1为自变量的终止值。

    3 椭圆曲线轮廓宏程序加工的应用实例
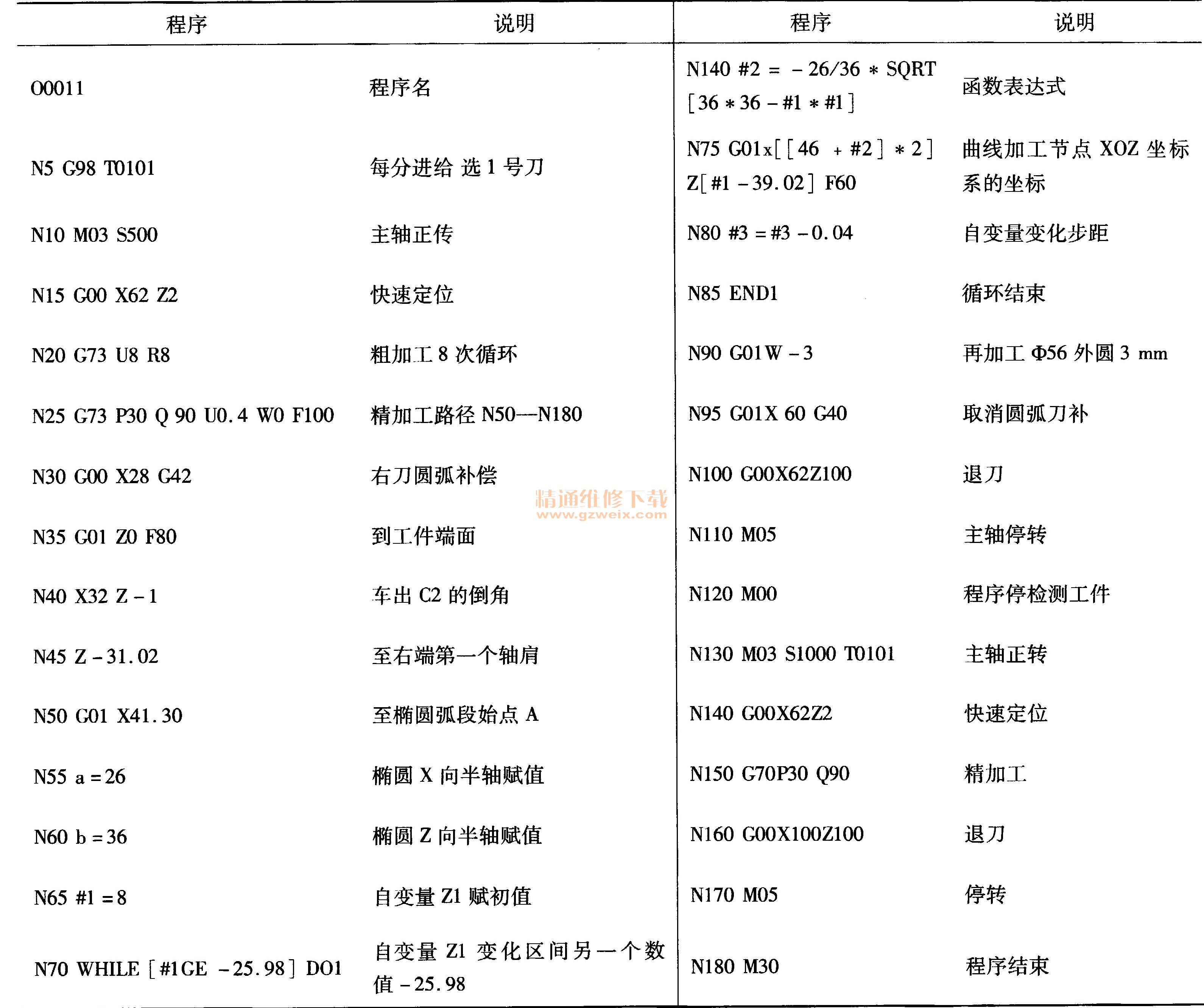
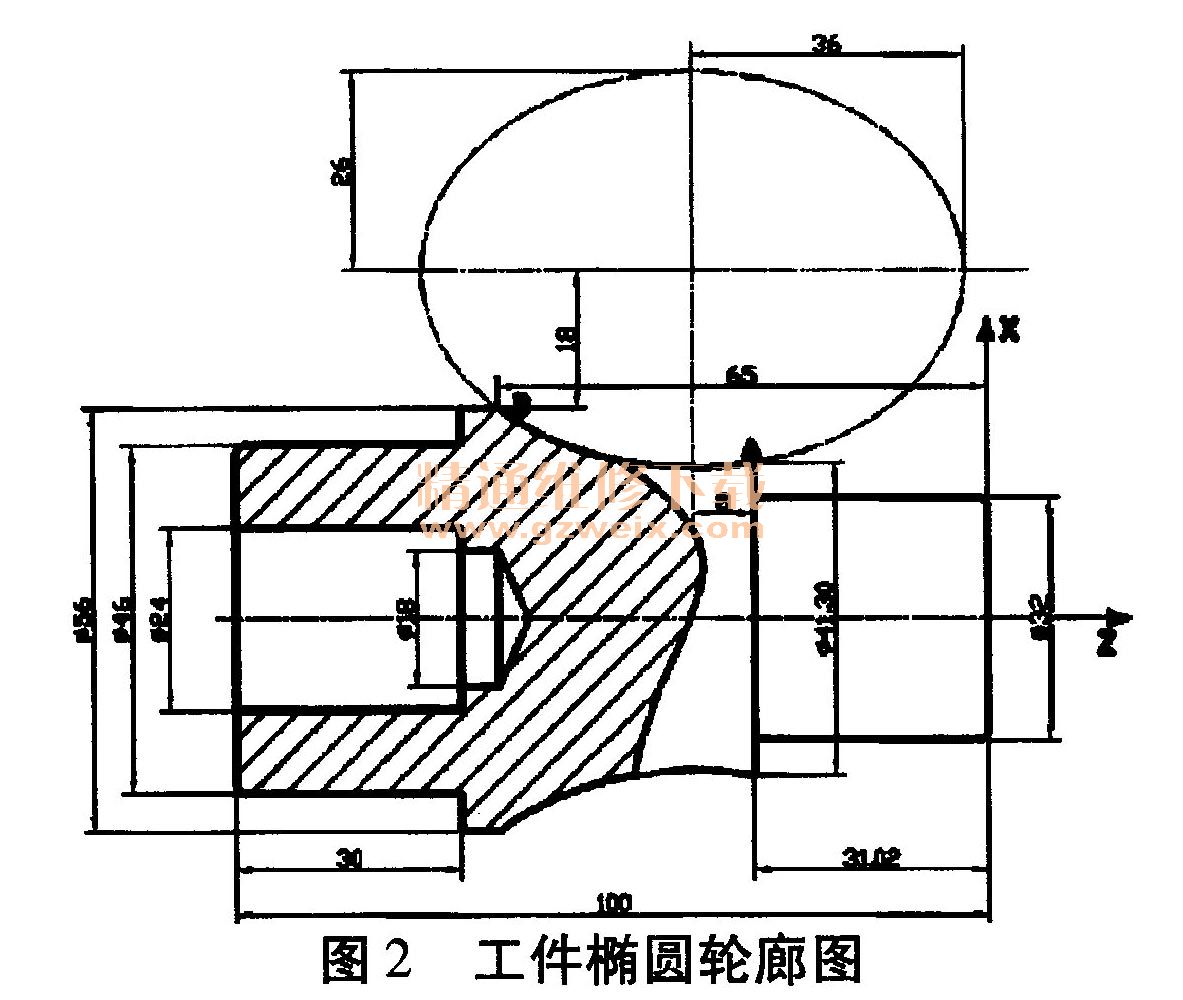
    依据上面的椭圆曲线宏程序模板，可以方便准确实现同类曲线轮廓的编程与加工。如图2所示工件椭圆轮廓，棒料直径：φ60 mm，在工件右端面建立编程坐标系XOZ。
    在X1O1Z1坐标系中，A点标准方程下的坐标值（－25.35，8） ，B点标准方程下的坐标值（－18，－25.98）。加工程序参考表如表2，加工零件图如图2。

    4 总结
    只要建立曲线宏程序模板，编程时只是改变参数而已，注意参数值的正负和变化特点，依据模板的格式，用上G71或G73指令，写出具体实例所需要的程序，模拟加工无误后真实加工即可。