·上一文章：剖析长城哈弗车全景环视影像系统
·下一文章：轻量化的镁合金引领电动车更轻盈（2）
2.2有限元计算的初始条件
有限元计算的初始条件包括材料、单元属性、施加约束和载荷等，该分析中涉及到超弹性材料的减震胶套、胶套与相连部件的接触，故使用非线性计算方法。
2.2.1材料特性
筒体主体结构和前后悬挂连接板采用普通的碳素结构钢ST12，分析中可以仅用杨氏模量和泊松比表示材料的应力一应变关系，其杨氏模量E = 210 000Mpa，泊松比v----0.28，密度P----7 800 kg/m3。
减震胶套是橡胶材料，材料的应力一应变关系是非线性的，并在外力作用下发生大位移或大应变，其材料性能接近于超弹性材料，对于超弹性材料，本构关系复杂，需用应变能W来描述材料特性。橡脸的本构模型种类很多，一般有二项Mooney-Rivilin模型、Neo-Hookean模型、Yeoh模型、Ogden模型等，均基于连续介质力学理论。其中二项Mooney----Rivilin模型不仅适用于经典的小变形线性弹性范围，而且适用于更大范围的形变；Neo----Hookean模型较为简单，在小应变内与试验结果吻合很好；Yeoh模型在较大应变范围内有很好的模拟结果；Ogden模型适用干小的或相当大的体积变化。因本文分析的减震胶套变形并不是很大，所以采用二项Mooney----Rivilin模型就可以得到很好的模拟分析精度。
二项Mooney-Rivilin模型应变能函数表达式为：
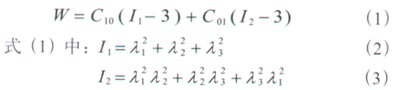
式（2）、 （3）中的λ1、λ2、λ3表示材料沿各边的伸长率。
C10和C01是材料常数，通过材料的基本试验获得。针对本消声器使用的减震胶套分别进行了径向和轴向力学试验，所得的曲线分别如图3、图4所示。
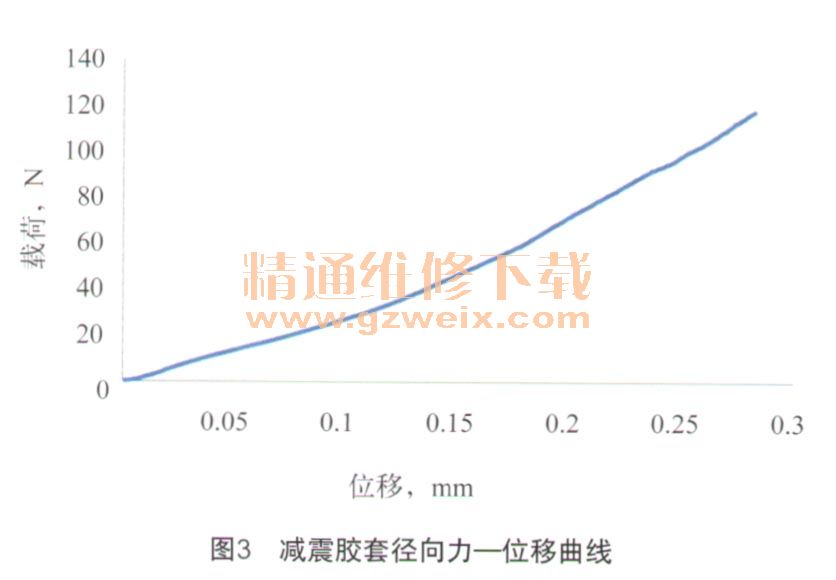
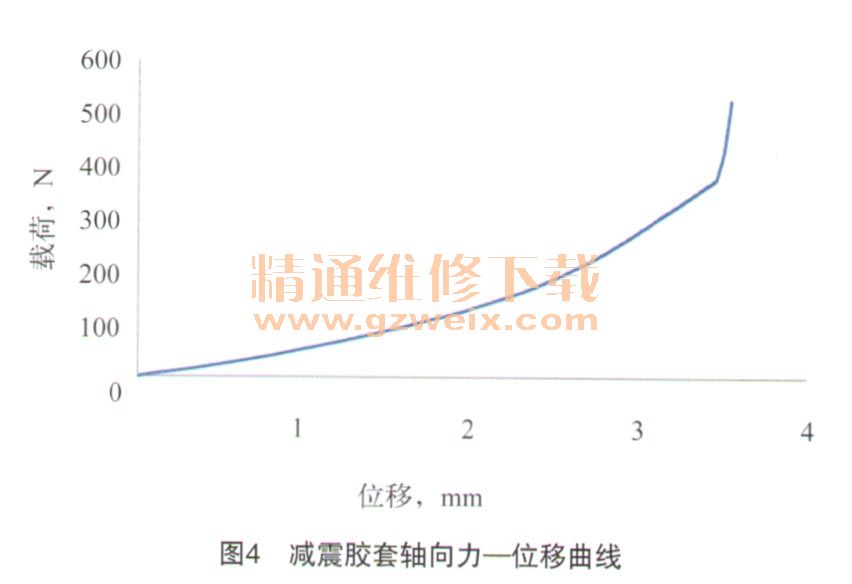
从图3和图4可以看出，在整个载荷加载过程中，胶套的径向刚度近似为线性状态；对于轴向刚度而言，载荷较小时为线性状态，加载到一定值时为非线性，当继续加载则胶套达到轴向限位状态，此时减震胶套的刚度取决干结构的刚度。
通过上面的胶套材料基本试验，结合最小二乘法理论拟合基于二项Mooney---- Rivilin模型的材料本构参数，获得C10=0.563 1，C01=0.046 23。
2.2.2边界条件
非线性有限元分析中边界条件的施加包括接触对的定义、载荷和约束的施加。
a）定义接触
结构中后悬挂采用柔性连接方式，该处的结构会影响到消声器其他区域的强度，故此处模型的建立是整个分析的关键之处。结构包括后悬挂支撑板、减震胶套、衬管、螺栓、简化的右脚蹬板外壳，模型中共建立了5个接触对：后悬挂支撑板一螺栓、后悬挂支撑板一衬管、衬管一螺栓、衬管一减震胶套、减震胶套－简化的右脚蹬板外壳，接触属性全部设定为沿表面法向受力。
b）约束边界条件
有限元计算时，为求解刚度位移矩阵，必须消除结构的刚体位移以保证刚度矩阵的非奇异，得到正确的数值解。合理选择节点并对节点自由度加以边界约束，是正确模拟消声器强度的关键。这里完全固定与发动机相连的排气管连接块、前悬挂支撑安装孔、简化的右脚蹬板外壳的自由度。
