摘要：应用有限元分析理论，建立了某款摩托车的频率响应分析模型，模拟了车架结构在发动机激励下的振动响应特性。在此基础上，以发动机的主倾角为设计变量、对骑乘舒适性影响比较大的几个关重点的振动加速度几何加权均方根值为目标函数，进行了结构优化计算，寻找最优的发动机一阶往复惯性力方向，以降低整车的振动从而提高乘坐舒适性，并为产品的研发提高理论参考依据。
    摩托车车架的主要功能不仅用于固定及支撑发动机、传动系统和悬架系统及其他相关元件等，还起着抑制来自前后车轮的各种负荷引起的扭曲变形，及为骑乘人员提供良好操纵稳定性和骑乘舒适性等作用。近年来，随着人们生活水平的不断提高，对摩托车性能要求也越来越高，尤其是乘坐舒适性。故车架除了应具有足够的强度和适当的刚度外，还应具有优良的动态特性。目前，产品设计阶段主要是用CAE分析技术来校核车架的强度和刚度，很少考虑结构动态特性及性能的优化，因此，开展摩托车结构振动特性研究对提高整车舒适性具有重要的工程价值和意义。
    摩托车在工作状态下，当外部激励频率与结构的某阶固有频率相同时，就会发生共振现象，这不仅影响车体结构的寿命，还严重影响乘坐舒适性和操纵稳定性。外部激励主要有路面不平度引起的随机激励力和发动机激励，本文主要研究摩托车在发动机激励下的振动响应特性，发动机激励包括气缸爆发压力、往复惯性力和离心惯性力等，而最主要的激励来源于一阶往复‘惯性力。
    本文以某款摩托车为分析对象，在简化整车3D模型的情况下，对车身结构进行有限元网格离散，并建立车架在发动机激励下的频率响应分析模型，获得对骑乘舒适性影响比较大的车架几个关重点在发动机常用转速范围内的振动加速度响应。在此基础上，以振动加速度加权平方根值作为优化目标函数、发动机的主倾角作为设计变量进行优化计算，以寻找最优的发动机装配角度。
    1  整车频率响应分析
    1.1有限元模型的建立
    为分析整车的动态特性，先对模型适当简化并建立主要零部件的有限元模型，包括车架、手把管、主副脚蹬、发动机、前后减震器及车轮等，本文主要研究车架结构在发动机一阶往复惯性力作用下的振动特性，因发动机激励通过车架与发动机悬挂连接板传递给车架，继而引起摩托车各部件不同程度的振动响应，整车结构中前后减震器起到一定的抑制作用，故在频率响应分析中主要建立车架、发动机、手把、前后减震器系统模型。
    摩托车车架与后叉主要由不同截面的管材和等壁厚的板材焊接而成[1]，结构比较复杂，在建立模型的过程中，由于各构件的厚度、壁厚相对于构件长度来说很小，并且壳单元相对于实体单元计算速度更快，从而采取抽取中面的方式建立了壳单元模型。
    前后减震器采用弹簧BUSH单元模拟，且均处于自由状态；主副脚蹬、手把管采用等刚度的杆单元模拟，发动机、车轮、骑乘人员采用质量点Mass模拟，各构件之间采用刚性单元MPC连接，由此建立的频率响应有限元分析模型如图1所示。

    1.2频率响应分析
    频率响应分析，是确定线性结构在承受随时间按正弦规律变化的载荷工况下的稳态响应分析[2]，主要分析摩托车整车在发动机整个转速范围内激励载荷作用下的振动特性，特别关注手把、主副脚蹬等关键部位处的振动情况，一般用这些部位的振动加速度大小、振动加速度RMS值、加权平方根值等随发动机转速的变化来描述。
    1.2.1载荷施加
    本文主要分析车架结构在发动机激励作用下的振动响应特性，发动机的激振力主要是由于发动机活塞、连杆、曲柄机构的不平衡质量产生的惯性力和惯性力矩引起的，对车架影响较大的是沿气缸轴线方向的一阶往复惯性力。该载荷可以通过发动机多体刚体动态力学来求解，获得发动机质心处在曲轴不同转速范围内的往复惯性力作为频率响应分析的输人条件，该分析中输入发动机在25~167 Hz范围内的一阶往复惯性力。
    1.2.2边界约束
    施加约束前，先建立整车分析坐标系，将整车前后行驶方向定义为x轴，垂直地面方向为z轴。分析中，为了消除刚度矩阵的奇异性，需按实际情况对结构进行约束处理；对于前轮轴处约束x、y、z方向的平动自由度，对于后轮轴处，为了协调车架的位移，此处释放x方向的平动自由度，仅约束y、z这2个方向的平动自由度。
    1.2.3频率响应分析结果
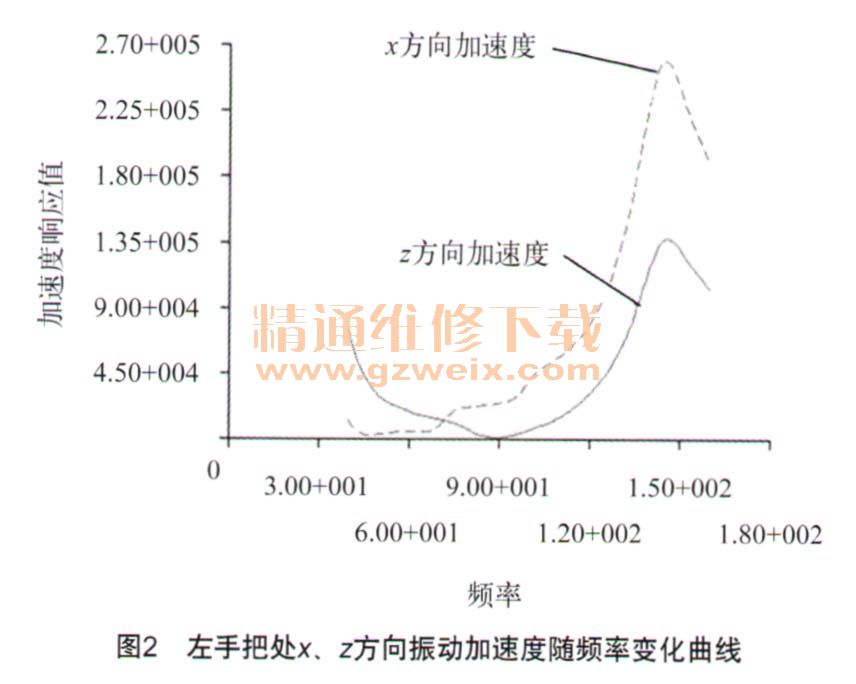
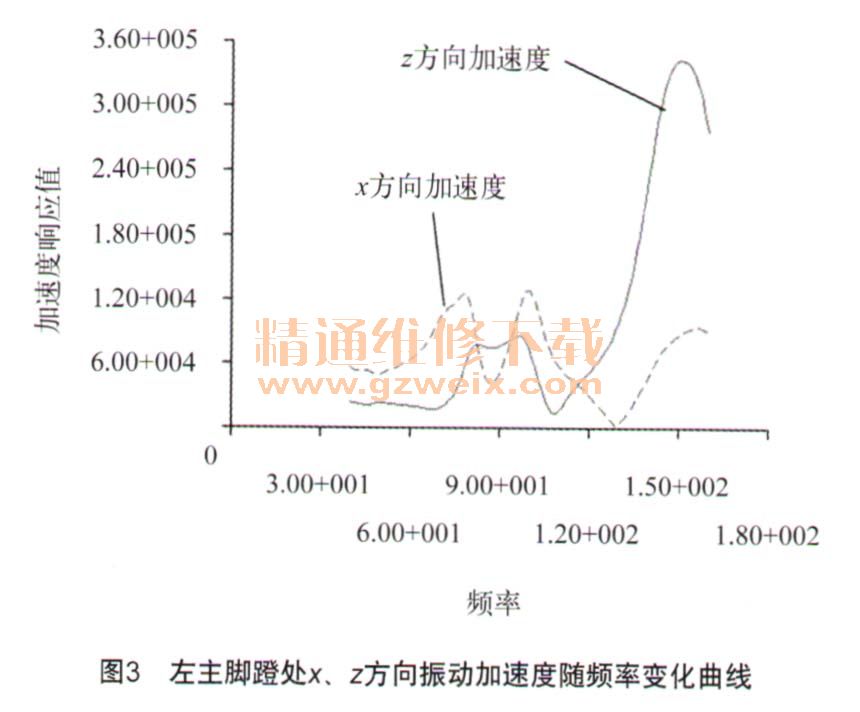
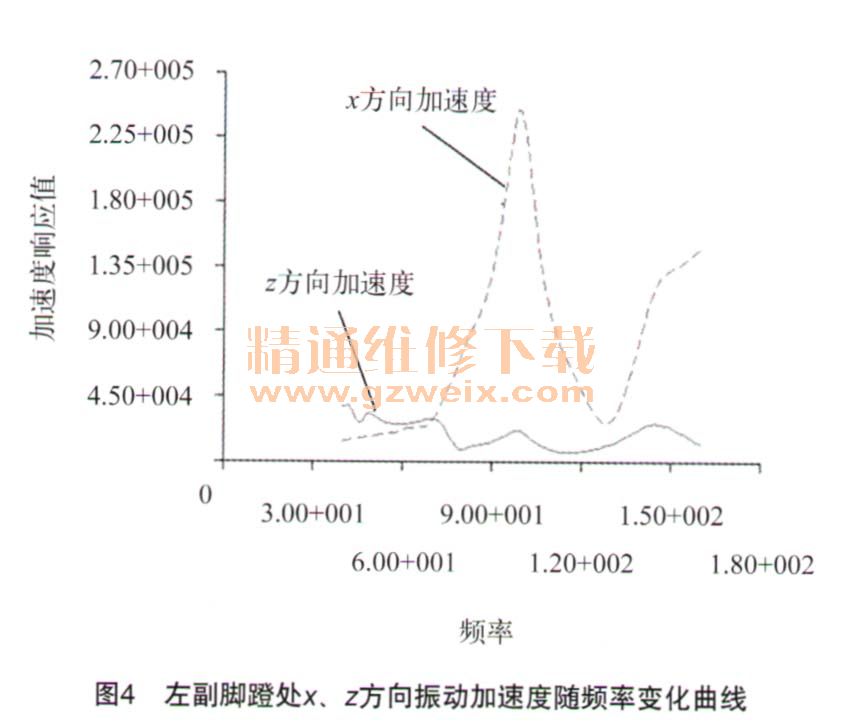
    对上述建立好的分析模型进行频率响应分析，每隔1 Hz为1个输出结果，分别获得左右手把、左右主脚蹬、左右副脚蹬处的振动加速度。因该车架结构左右部分基本对称，其振动加速度在发动机激励下的变化规律相似，故本文只列出左手把、左主脚蹬和左副脚蹬的频率响应分析结果，如图2~图4所示，图中x轴为频率变化范围，Y轴为摩托车关键点在对应频率下的加速度响应值。
    从图2~图4振动加速度随频率变化曲线看到，左手把约在146 Hz出现峰值，x方向的振动加速度约为26 g，z方向的振动加速度约为14g；左主脚蹬处约在101 Hz时x方向出现峰值，振动加速度约为13 g，约在152 Hz时z方向出现峰值，振动加速度约为34 g；左副脚蹬处约在100 Hz时x方向出现峰值，振动加速度约为24 g，在发动机整个转速范围内z方向的振动较小。





    2 发动机最优主倾角优化
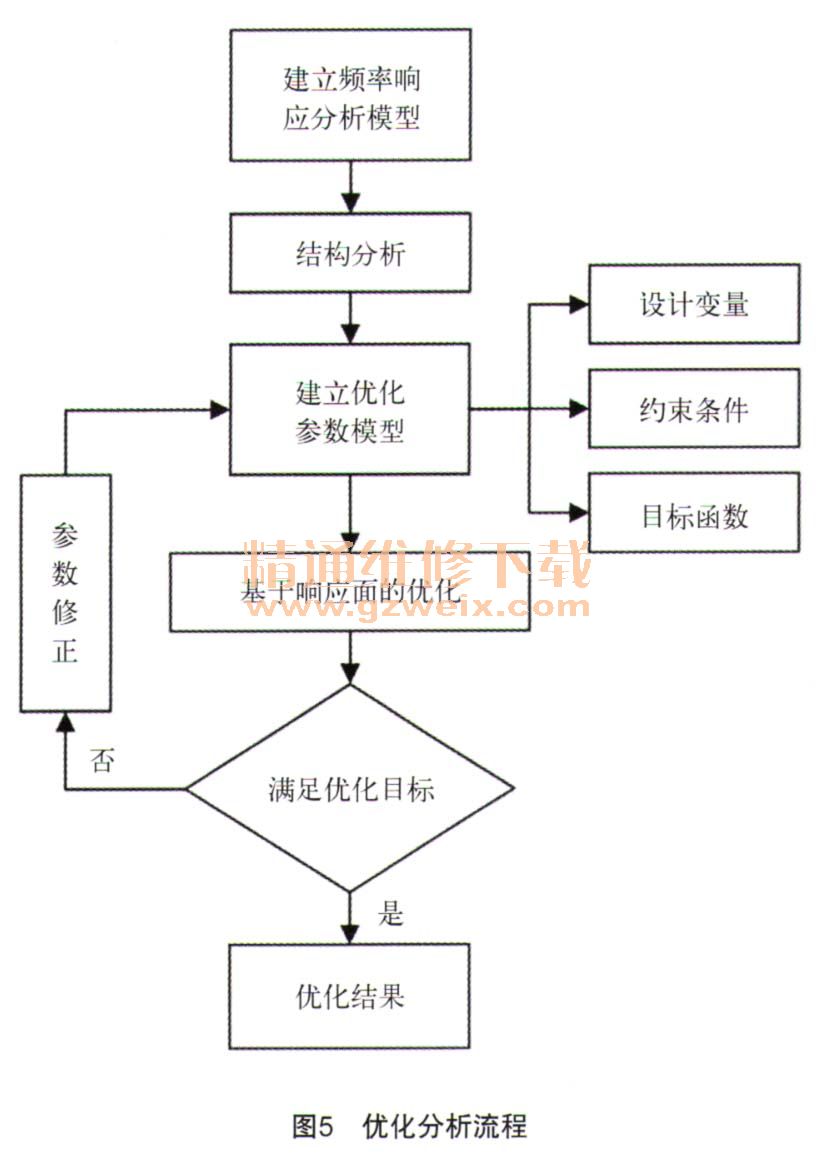
    结构优化分析是指在给定的系统描述和目标函数下[3]，拟定一组设计变量，使目标函数最优（最大或最小），优化分析中通常包含3个要素：设计变量、约束条件和目标函数，本文的优化设计流程如图5所示。

    2.1设计变量
    影响摩托车振动性能的因素主要有摩托车结构形状、外部的激励（路面激励、发动机激励）、摩托车与发动机间的匹配关系等。目前，有限元优化技术在振动性能中的应用主要是针对摩托车车架结构的优化，涉及结构尺寸的优化有管材的外径、壁厚及加强板的
壁厚参数等。本文主要研究发动机激励对摩托车振动加速度的影响，而发动机激励包括载荷的大小及方向，下面以发动机主倾角（涉及激励载荷的方向）为参数变量对影响骑乘者振动舒适性的几个关重点进行优化分析，便于角度定义，文中将发动机一阶往复惯性力方向与z轴（垂直地面方向）的夹角定义为设计变量。
    2.2目标函数
    经综合考察车架左右上手把位置、左右主脚蹬、左右副脚蹬6个点在发动机常用转速范围内的振动情况，而不是针对几个频率点进行振动优化，将6个点的振动加速度进行几何加权均方根值处理：
37页公式
    式中：aki----在频率k时测点i的振动加速度
      l、u----分析频率范围的下、上限
      i----左右上手把、左右主脚蹬、左右副脚蹬位置点
    优化前6个测点的振动加速度几何加权均方根值为9.2 g，综合考虑这几个位置点对振动舒适性的影响，将加权平方根值定义为振动优化设计目标函数。
    2.3优化计算
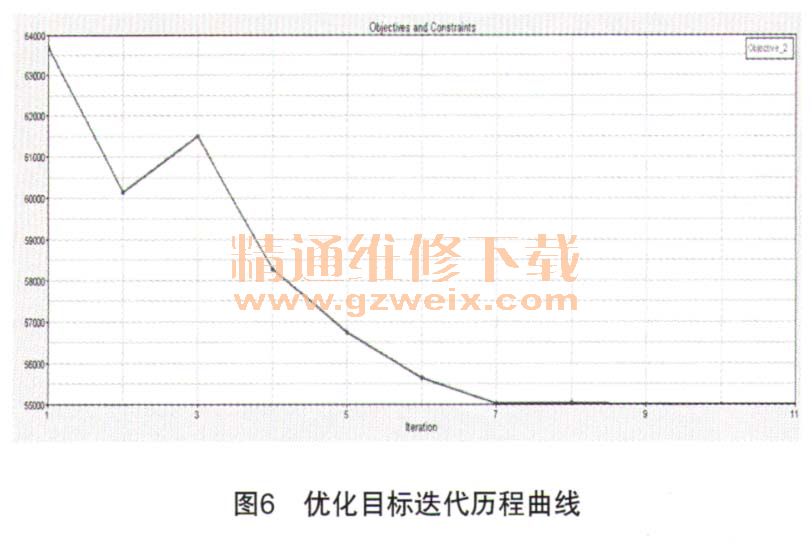
    将上述定义好的参数优化模型采用自适应响应面法进行优化计算，得到的优化目标迭代曲线如图6所示，从优化结果中可以获得：当发动机一阶往复惯性力方向与：轴夹角为57°时，6个测点在发动机常用频率范围内的振动加速度几何加权均方根值最小，其值由原来的9.2 g降为7.9 g。

[1] [2]  下一页