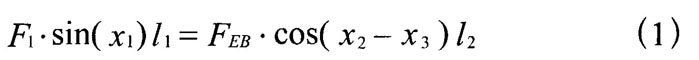
式中：F1—施加到变挡杆的作用力，N
      X1—变挡杆与水平线的夹角，（。）
      FEB—变档杆作用于变挡力臂的力，N
      x2—变挡摆臂与竖直方向的夹角，（。）
      x3—变档杆与水平方向的夹角，（。）
      l1—变档杆理论作用长度，mm
      l2—变挡摆臂作用长度，mm
    按图4的力学模型，施加于摆臂的作用力FEB产生的力矩要大于变挡轴的变挡力矩Mo，即：

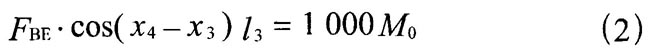
式中：FEB—变挡拉杆作用于变挡轴的作用力，N
      x4—摆臂与竖直方向夹角，（。）
      13—摆臂作用长度，mm
      M0—发动机换档力矩，Nm
    由式（1）、（2）可知：

即

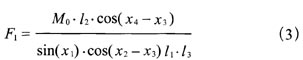
    因为x1 ≠0， x2、 x：均为锐角，l1\13≠0，所以（3）式分母不为0。

    4 利用MATLAB求目标函数最优解
    4.1目标函数及边界条件
    a）目标函数：根据图2可知，在实际换挡过程中，如果变档摆臂与摆臂相互平行，根据理论力学可知，变挡拉杆将做平行运动，此时，变挡拉杆不会产生转动惯量，换档就会轻松。故，在实际设计当中，要保持二者平行布置，即x4＝x2，所以（3）式可以简化为：

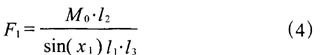
b）边界条件：
l1、l2、13＞0    （5）
0°＜x1＜90°   （6）
L1、l3≤3200 l2  （7）

    4.2  MATLAB优化算法
    MATLAB软件提供了多种优化算法，MATLAB可以直接调用这些优化函数进行最优解计算。本文采用fmincon优化函数进行最优求解，调用的程序算法如下。

    实例计算：以某型号发动机手变挡操纵机构为例进行计算，

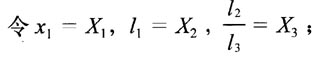
    在MATLAB程序中，利用上面程序，带入数据。求得最优值时X1=1.6，X2＝544.28，X3＝1.7，F1＝6.2。

    5 结论
    a）本文通过对实际手变挡模型的简化，利用整体法建立了正三轮摩托车手变挡机构的力学物理模型，并通过力学分析建立了手变挡机构的受力方程。
    b）利用MATLAB提供的优化算法，对建立的手变挡机构的力学方程在边界条件下求得了参数的最优解。
    c）通过实例计算，验证了本文方法的正确性和可行性，为手变挡机构的设计提供了参考依据。

上一页  [1] [2]