2 模态优化
    2.1模态分析
    利用有限元分析软件ANSYS Workbench建立车架的有限元模型如图5所示，仿真模型中略去了一些线夹、小支承、焊接螺母等小结构，零部件的连接通过ANSYS Workbench建立焊点实现。

    计算得到车架的前20阶模态频率值如表1所示，因在前处理中没有对车架进行约束，所以计算的前6阶频率值为0，第7阶模态即为对应的一阶模态，其余模态依次类推。

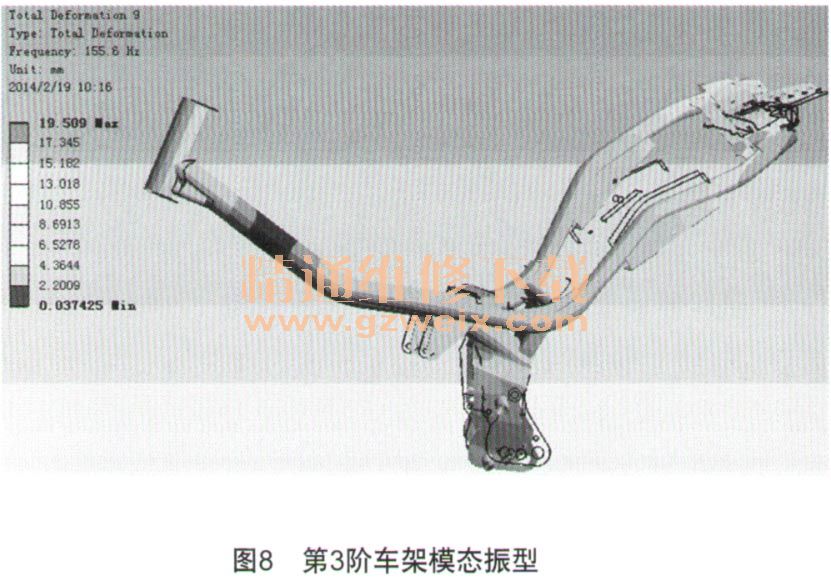
    仿真得到的前4阶振型图如图6～图9所示，第1阶振型为以中轴线为支点呈前后弯曲变形，第2阶振型为发动机悬挂板的前后摆动变形，第3、4阶振型为车架两侧管的扭转变形。

    2.2仿真计算值与试验值模态对比
    车架实测频率与计算频率对比如图10所示，由图中看到，ANSYS Workbench计算得到的车架固有频率与试验测得的频率相比，误差均在5％左右，这主要是在仿真模型中略去了一些次要的支承件，总的来说，在几个低阶模态中，二者吻合的较好。另外，理论计算得到的频率要比试验测得的模态数略大，这主要是跟试验中传感器的布置位置有关，加之试验条件有限，从而丢失了一些模态。

    对比图4和图6看到，仿真得到的振型图与试验测试结果一致，即在低频段，车速50 km/h下，振动较大的部位出现在手把和车架尾部，该结果验证了摩托车在行驶速度50 km /h下，发动机的激励频率73.8 Hz与车架的一阶固有频率接近，引起了结构共振。
    2.3结构优化
    由于车架在一阶固有频率下的变形为弯曲变形，所以优化的目标为提高车架的抗弯刚度，从而使车架的固有频率与激励频率避开。为提高车架的抗弯刚度，在车架的两侧管上添加了2个加强管如图11所示。

    对优化后的结构重新通过有限元仿真计算，得到车架的固有频率为109.87 Hz、181.26 Hz、222.7 Hz、247.08 Hz，对一阶频率而言，优化后的车架的频率较优化前提高了40％左右。经试制，路试测试后，优化后的车架较原车架有较大改善。

    3 结论
    针对摩托车研发过程中经常遇到的振动问题，通过试验测试和有限元仿真相结合的方法，提供了一种行之有效的解决途径，对解决摩托车设计过程中的振动问题具有一定的参考意义。
 

上一页  [1] [2]