摘要：通过分析凸轮升程误差曲线的变化规律，提出用于修正对称凸轮和不对称凸轮在测量时，因位置误差的影响而歪曲的升程误差值的2种方法，即图解法和解析计算法。

    凸轮轴是摩托车发动机的核心部件，其功能是保证发动机正确的配气相位和按一定的规律控制气门组定时开、闭。凸轮轴上各凸轮的尺寸和形状误差，是影响气门定时开闭间隙大小和配气效率的主要因素，在发动机设计、制造的整个过程中，允许对凸轮进行检测，以保证凸轮的几何精度和装机后的动力性能。
    可是在实际测量中，不可能事先知道哪一个值是最小的，也不可能把所有的值都一一求出来，然后从中找出最小值，所以，必须找出一种能被公认的求解那个转角误差最小值的便捷方法。
    测量实践表明，“敏感点法”不但测算过程简便，而且能满足发动机凸轮的检测要求。“敏感点法”所获得的升程误差检测数据，在实际运用中符合“最小条件”原则，它是凸轮检测的理想方法之一。

    1.凸轮升程误差曲线变化的规律性
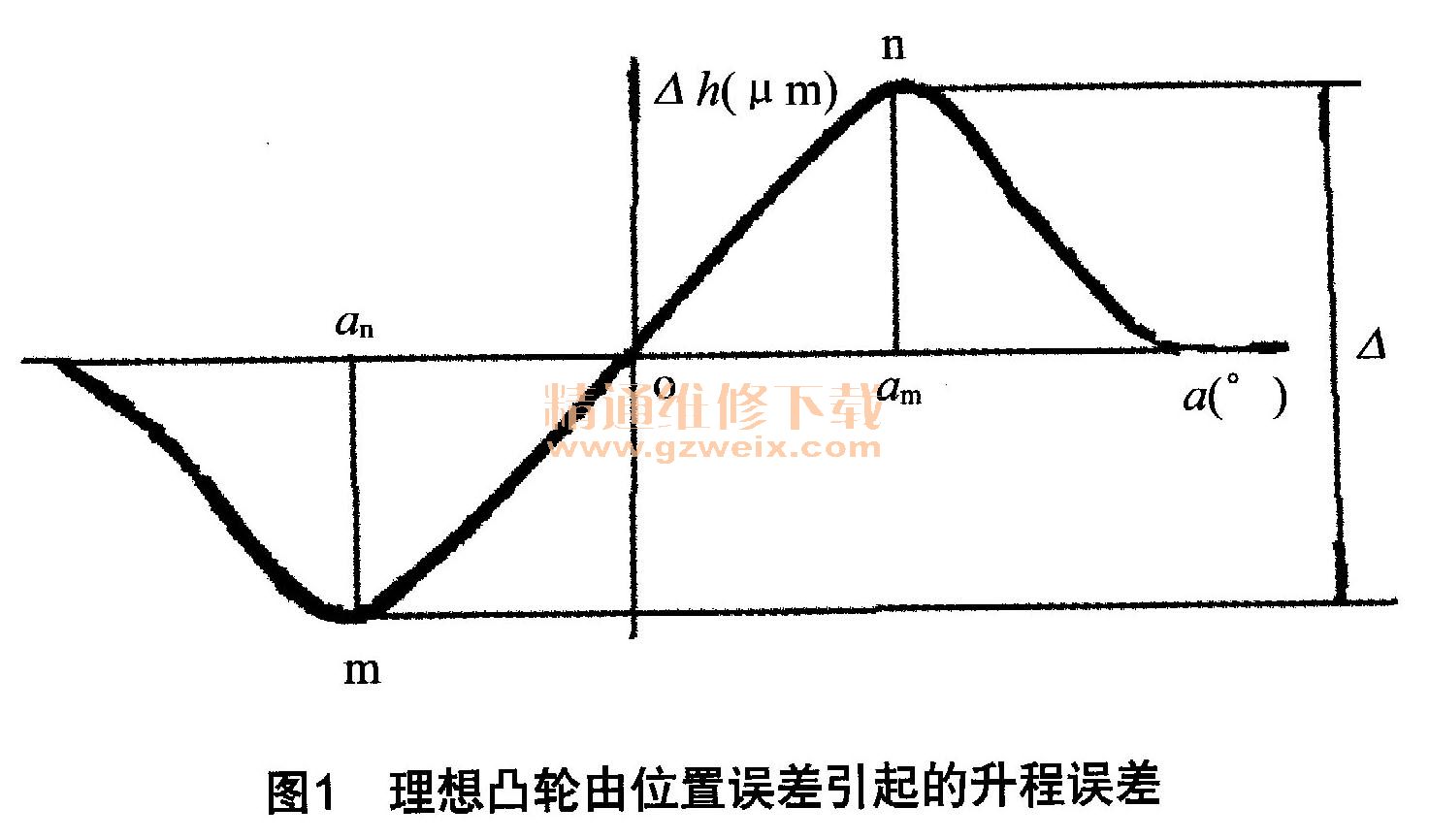
    理想凸轮的升程误差曲线本应是1条和横轴重合的直线，如果测量时凸轮的位置（起始转角）有一误差△a，这就使本来没有误差的理想凸轮出现了升程误差，其包容宽度为△，如图1所示。

    凸轮升程曲线，应以连续函数的形式给出，即：
                    h =f（a，r）（1）
    式中：h—凸轮被测点升程
      a—凸轮被测点转角
      r一凸轮被测点曲率半径
    位置误差引起的升程误差如图2所示，分析图2曲线族可以看到：1）由△a引起的升程误差曲线是1条按升程变化律变化的曲线；2）凸轮的“桃尖”两侧升程误差曲线变化方向相反；3）不同的转角误差，对应不同的升程误差曲线，转角误差越大，曲线越陡；4）转角误差符号相反，升程误差曲线的峰谷相反。

    2 升程误差曲线的鉴别
    凸轮的升程误差，是由升程误差曲线中误差包容区域最小为△1的曲线来确定的，可在实际测量中，不可能事先知道哪个△的值（或哪条曲线误差包容区域）最小。理论和实践均证明，凸轮升程误差符合“最小条件”时，凸轮处于最佳位置，这时，凸轮升程误差曲线真实地反映凸轮的形状误差。得到如下“最佳曲线”的“鉴别准则”有：1）升程误差曲线上，必须具有异侧等值误差极限点；2）单值误差极限点的升程变化率绝对值，必须在异侧等值两误差极限点升程变化率的绝对值之间。

    3 凸轮升程误差曲线的校正
    凸轮升程误差曲线的校正，是为了剔除位置（转角）误差的影响，得到真实反映凸轮形状误差，即符合“最小条件”的最佳升程误差曲线。
    3.1升程误差曲线的图解校正方法
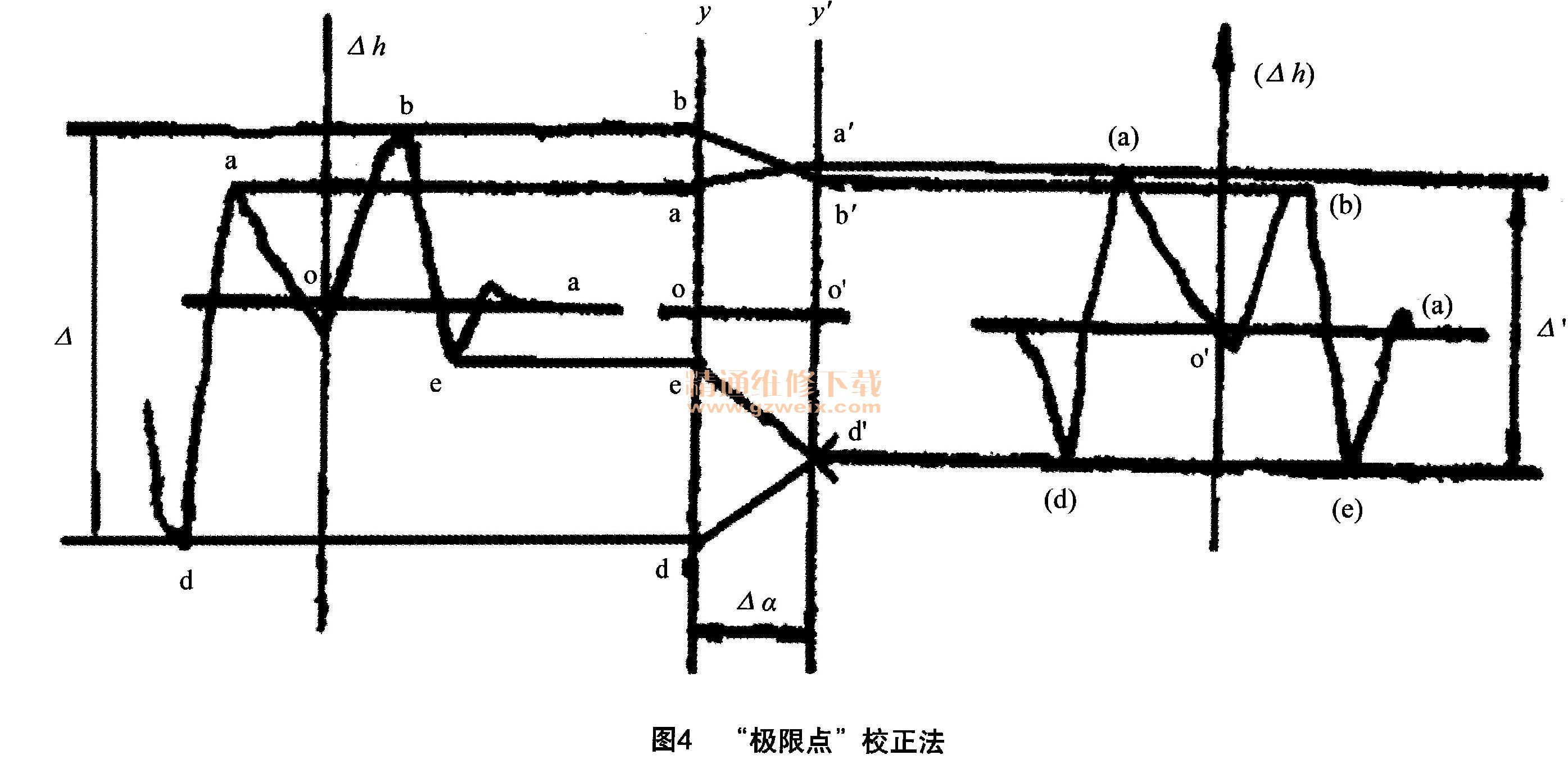
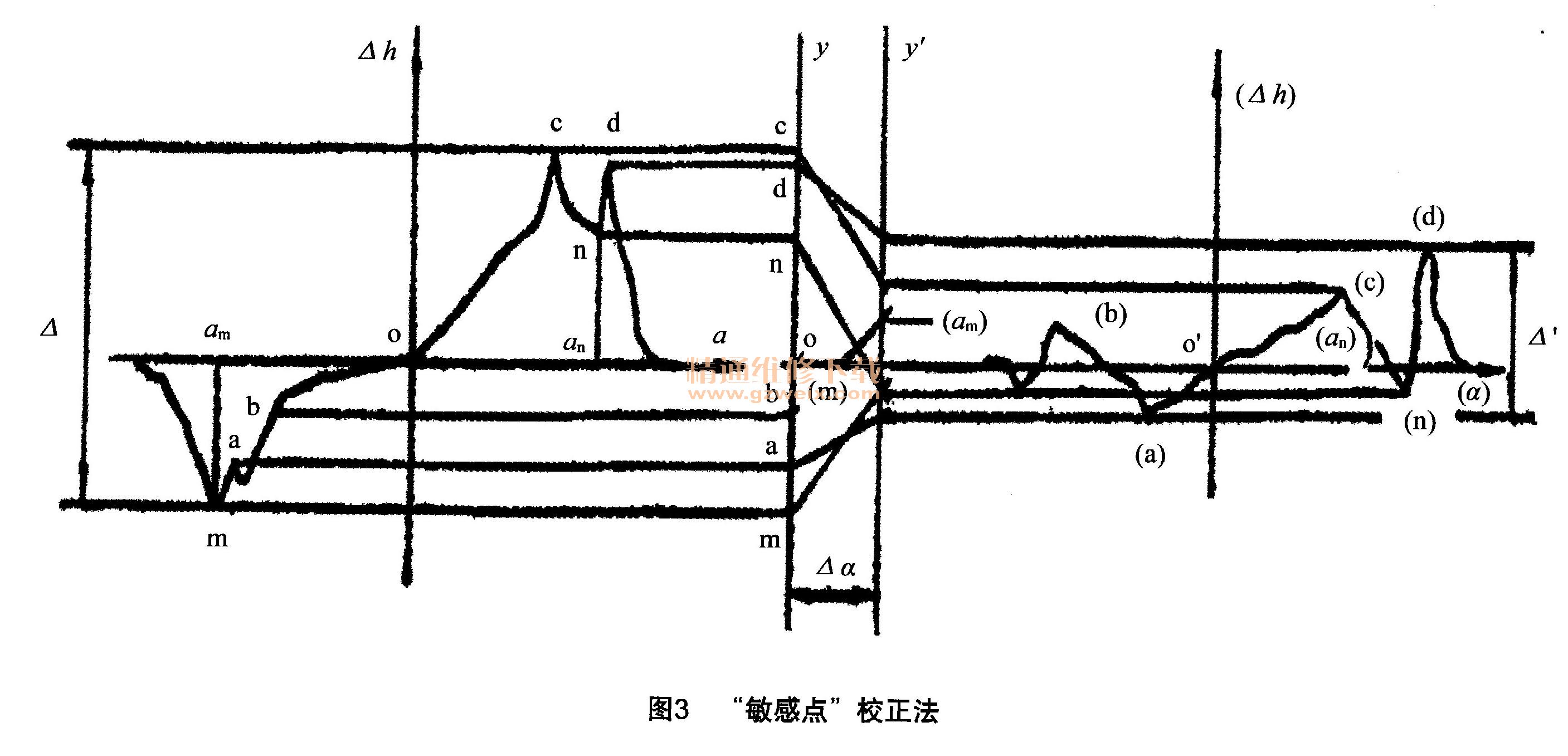
    a）“敏感点”校正法：“敏感点法”是依据凸轮两侧“敏感点”m和n升程误差相等，即△hm=△hn时，建立校正基准的。图3中Y是测量基准，Y1是校正基准（评定基准），作图时把曲线上的敏感点m和n投影到Y轴上，作出两侧“敏感点”m和n的校正轨迹直线（其斜率与该点升程变化率的大小和符号相同），过两校正轨迹直线的交点引Y＇平行于Y，YY＇间的距离就是转角校正值。这时，将曲线上其余各测点投影并作出校正轨迹直线，各校正轨迹直线与Y＇的交点，就是校正曲线上的误差点，还原后就得到了凸轮的校正升程误差曲线，具体操作方法如图3所示。

    b）“极限点”校正法：依据最小条件原理，使凸轮两侧同名各误差极限点a和b相等建立基准的。作图过程和“敏感点法”基本相同，只是把“敏感点”换成“极限点”，并从异侧同名各误差极限点中选择符合“准则”的那一对极限点校正轨迹直线的交点，确定转角校正量和建立校正基准。具体操作方法如图4所示。

[1] [2]  下一页