3.2升程误差曲线的解析校正方法
    a）校正轨迹直线方程式：如图5所示，将升程误差迭代数据中的极限点a、 b、c、d投影到直角坐标系xoy纵轴Y上，作出a、 b、c、d各点的变化轨迹直线，由解析几何可知各直线的方程式（斜载式）如式（1）所示。

                      h=kx+b（1）
    式中：k一轨迹直线的斜率，大小和符号与被测点的升程变化率相同
      b—变化轨迹直线的纵载距
    b）等值误差极限点的获得和转角校正值的确定：为了获得符合“最小条件”要求的升程误差值，依据“敏感点法”原理，使凸轮左、右侧误差极限点（最大或最小点）等值，这时，必须通过改变凸轮测量起点转角来实现，具体方法是确定它们的变化轨迹直线交点坐标。如左右侧最大点a和b等值时，约束条件为|ka| φ| kc或d|π|kb|（当使左右侧最小点c和d等值时，其约束条件为|kcφ|1 ka或kb|π|kd），这里需说明的是，对于约束条件的中项a或b，取其中误差值大的点（c或d取其中误差值小的点），根据式（1）可得：

    解式（2）方程式，可得a和b交点坐标：

    将式（3）各参数对照图4凸轮参数名称进行置换，得到：

    式中：△a—凸轮转角修正值，也称坐标旋转角
      △ha、△hb，△h（a）、d h（b）—误差极限点a、b转角修正前、后的升程误差值
      ha '、hb'—误差极限点a， b的升程变化率
    C）误差极限点的验证：转角校正前的误差极限点，校正后是否仍是极限点，应按下式验证：

    当任意点的升程误差满足式（5）时，说明转角校正值前、后极限点没有变化，否则应按校正后新的极限点重新计算。
    d）转角校正后升程误差值的计算及二次测量方法：转角校正后凸轮各测量点符合“最小条件”要求的升程误差值，按下面解析式计算：

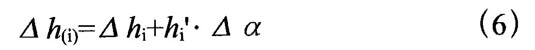
    也可以按校正后的起点转角φ（0）= △0+ △a进行二次测量，获得凸轮各测量点符合“最小条件”要求的升程误差值△ h（i），在企业中一般推荐采用二次测量方法。
    e）求解凸轮升程误差曲线的最小包容区域：在确认符合“准则”后，根据“最小区域法”，凸轮升程误差曲线的最小包容区域△ （min）按下式计算，即：

    式中：△h（max）、△h（min）—凸轮所有测量点中升程误差值的最大、最小值
    最后指出的是，本文所给出的各种凸轮升程误差曲线的校正方法，适应干对称凸轮，同样也适应干不对称凸轮。
 

上一页  [1] [2]