分析摩托车车轮疲劳寿命

来源：摩托车技术作者：佚名 2014-08-04 10:30:28

摘要：用有限元分析法，对摩托车车轮旋转弯曲疲劳试验和扭转疲劳试验进行了分析计算，得到了车轮在旋转1周内的应力分布情况，并在此基础上校核了车轮在试验工况下的疲劳寿命，为结构的可靠性设计提供了参考依据，为旋转体结构的疲劳寿命分析提供了有效的方法。

    车轮是摩托车的行走部件，起着承载、行驶、转向、驱动和制动等功用，承受在此行驶过程中所产生的弯曲、扭转和冲击等各种复杂载荷。可见，车轮性能的好坏直接影响摩托车的行驶安全性、平顺性、稳定性和牵引性。为保证车轮具有足够的强度和刚度，现已将有限元分析技术应用到结构设计中，但较多的是采用静强度校核法，由于大部分机械结构的破坏属于疲劳失效，故有必要对车轮进行疲劳可靠性分析。疲劳分析法是用来处理动应力及由此产生的破坏方式的基本方法，主要用来研究结构的应力状态与寿命之间的关系，从而确保车轮在动载荷作用下的疲劳强度，以提高结构的可靠性。
    本文以某款车型的车轮作为分析对象，运用有限元理论，建立准确合理的车轮结构力学模型，模拟车轮在旋转弯曲疲劳试验和扭转疲劳试验工况下，不同旋转角度所对应的车轮应力分布情况，并在此基础上利用名义应力法和累积损伤理论，根据试验获得的材料疲劳特性曲线，探索旋转体的疲劳寿命分析方法，预测疲劳耐久性能，从而为结构的合理设计提供理论参考。
    1 车轮有限元建模
    本文分析的车轮为压铸整体式结构，主要由轮毂、轮辐和轮辆组成，因该结构为不规则体，在建模时采用四面体单元进行离散；将旋转弯曲疲劳试验和扭转疲劳试验中的载荷臂简化为等刚度杆单元，采用多点约束单元MPC模拟载荷臂与车轮之间的装配关系，由此建立的有限元分析模型如图1所示。

该车轮采用ZL101A材料，弹性属性为：弹性模量E = 7.5×104 MPa，泊松比μ = 0.3，密度ρ=2.8×103 kg/m3。

    2 车轮疲劳分析
    2.1分析理论
    本文采用名义应力法对车轮进行疲劳寿命分析，该方法适用于外加应力名义上、在材料的弹性范围内、且结构的失效循环次数很高，位于高周疲劳区域内时的分析。该分析方法以材料或零件的S-N曲线为基础，对照试件或结构疲劳危险部位的应力集中系数和名义应力，结合疲劳累积损伤理论，校核疲劳强度或计算疲劳寿命。
    车轮属于旋转体，该结构的特点是承受的载荷是沿着旋转体外围传播的，通过载荷施加到车轮连续扇区上完成仿真分析的，兼顾因作用力施加次数不足造成分析误差过大或次数过多导致分析时间过长的因素，将作用力的作用周期等分为36等分，即作用力与作用力之间相隔10°，并依次施加，完成一个完整的作用力周期。这样，可以绘出载荷施加到车轮连续位置上每一个节点所对应的应力一历程。通过载荷工况的应力结果，可以确定旋转变化的每个节点的一个完整的应力时间历程和疲劳损伤。
    2.2静强度分析
    静强度分析的目的是，将应力分析结果作为疲劳分析的一个输人参数，并根据结构的最大应力，选择合适的疲劳分析方法。本文强度校核主要模拟车轮在试验状态下的应力分布情况，施加的边界条件与试验固定方式及加载工况一致，并按照GB/T 22435-2008《摩托车和轻便摩托车轻合金车轮》标准要求，进行旋转弯曲疲劳试验、径向载荷疲劳试验、径向冲击试验、扭转疲劳试验和静负荷性能试验。本文主要分析旋转弯曲疲劳试验和扭转疲劳试验2种情况。
   2.2.1旋转弯曲疲劳试验工况
    该试验中，车轮可在一固定不变的弯矩作用下旋转，或车轮静止不动，承受一个旋转弯曲力矩作用，施加的弯矩M值由式（1 ）确定，建立的车轮在旋转弯曲试验工况下的有限元计算模型如图2所示。

                  M＝0.7μ·Fv·r           （1）
式中：M----弯矩
      μ----轮胎与路面的摩擦系数
      Fv‑---车轮设计时规定的最大垂直载荷或额定载荷
      r----轮胎最大静力半径
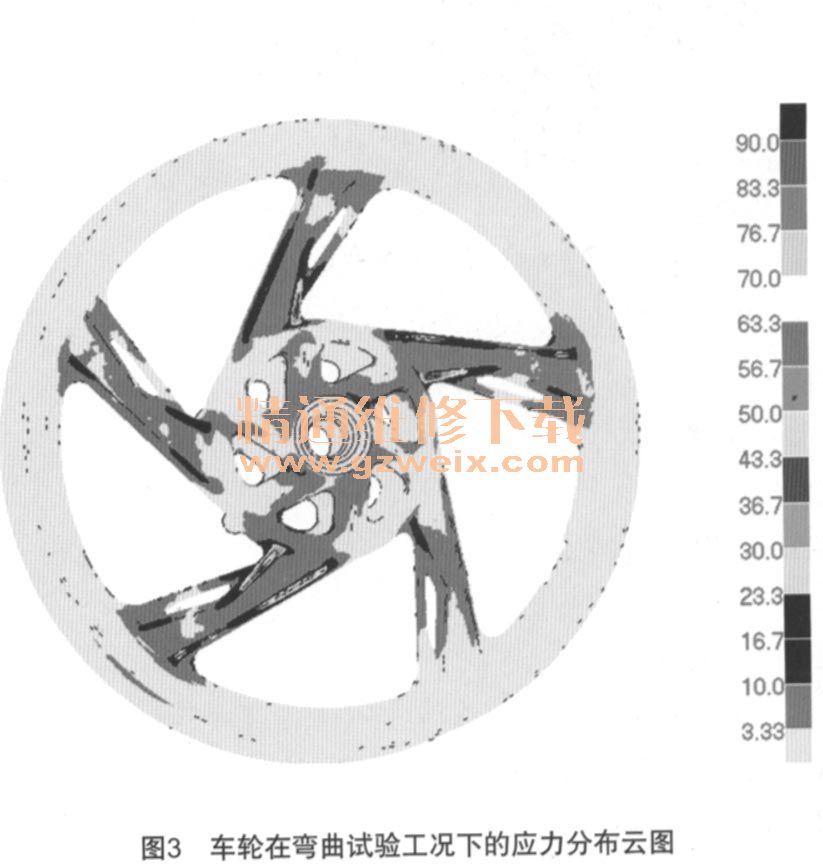
    通过分析计算，得到车轮在一个完整载荷作用力周期下的应力分布云图，图3为车轮在弯曲载荷作用过程中，某个转动角度处的整体应力分布情况。
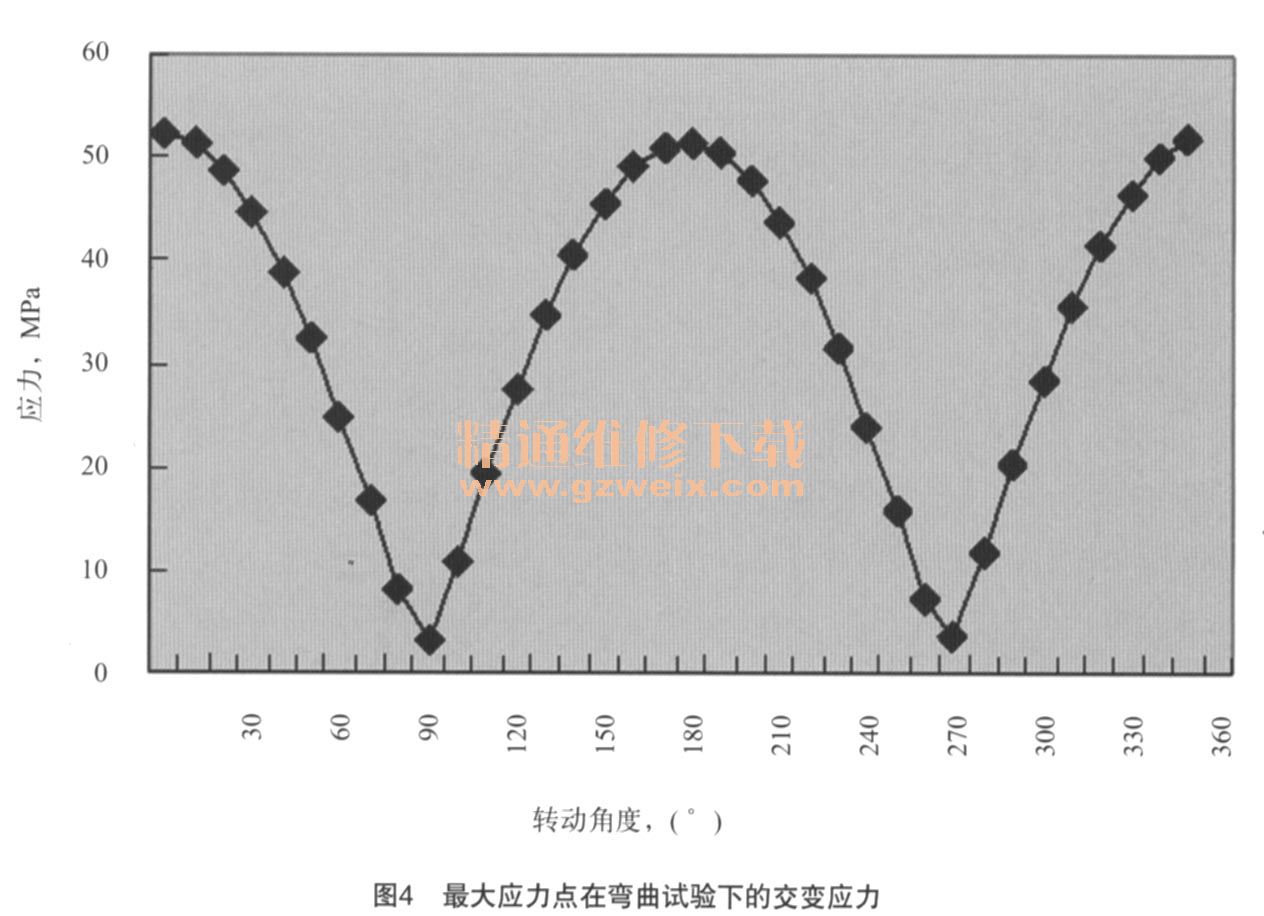
    由图3看到，弯曲试验载荷在该转动角度时，车轮轮辐倒角处存在相对应力集中区域，此时，结构的最大应力为52.5 MPa，小于材料的屈服强度极限。图4为车轮最大应力点在弯曲试验工况下旋转1周内的应力变化。

    2.2.2扭转疲劳试验工况
    在该试验中，车轮可在一固定不变的扭转力矩作用下旋转、或车轮静止不动，承受1个旋转扭转力矩，该力矩施加在轮毂和轮辆之间，施加白Na转力矩T值由式（2）确定，由此建立的车轮在扭转疲劳试验工况下的有限元计算模型如图5所示。

                      T＝±Fv·r（（2）
式中：T----弯矩
      Fv----车轮设计时规定的最大垂直载荷或额定载荷
      r----轮胎最大静力半径
    采用与弯曲试验工况相同的分析计算方法，获得车轮在一个完整的载荷作用力周期下的应力分布云图。在与上述弯曲试验相对应的相同转动角度处，在扭转载荷作用下，车轮的整体应力分布情况如图6所示。

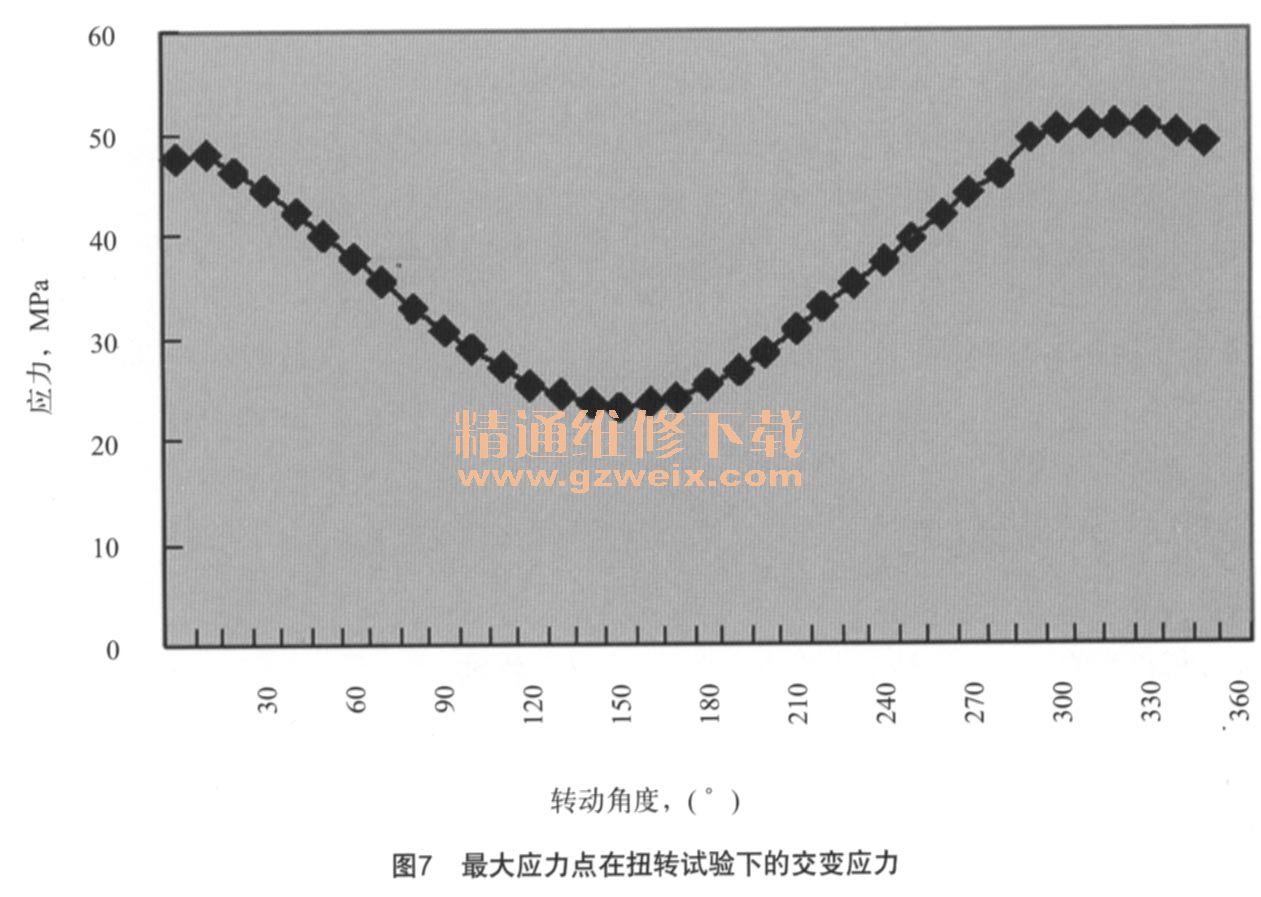
    由图6看到，扭转试验载荷在该转动角度处，车轮轮辐倒角、轮毂局部存在相对应力集中区域，此状态下结构的最大应力为47.6 MPa，小于材料的屈服强度极限。图7为车轮最大应力点在扭转试验工况下旋转1周内的应力变化。